|Z^2+2iz-1|<9
Sys: |Z2+2iz−1|<9
Δ=i2+4=3
Z1=−2i−√32= − √32−i
Z2=−2i+√32= √32−i
|[Z−(− √32−i)][Z−(√32−i)]|<9
Wiem jak zaznaczać w postaci |Z−Z0|. Jak poradzić sobie tutaj.
16 lis 16:19
PW: Źle liczysz wyróżnik Δ.
Podpucha, zwykły wór skróconego mnożenia:
|z2 + 2iz + i2| < 9
|(z+i)2| < 9
i równoważnie
|(z+i)2|2 < 81.
Jeżeli oznaczymy
z = a + bi,
to
z + i = a + (b+1)i
(z + i)2 = a2 − (b+1)2 + 2a(b+1)i
|(z + i)2|2= ((a2 − (b+1)2)2 + 4a2(b+1)2.
Mamy rozwiązać nierówność
((a2 − (b+1)2)2 + 4a2(b+1)2 < 81
Co to będzie na płaszczyźnie zespolonej? (trochę przekształcić).
16 lis 16:44
Sys: Faktycznie zapomniałem o 22 licząc Δ, za chwilę przekształcę to.
16 lis 16:49
Sys: Z jakiej reguły podnosimy moduł do kwadratu? Niezbyt rozumiem tę zależność.
16 lis 17:47
PW: Z definicji.
|u + vi|2 = u2 + v2
16 lis 17:49
Sys: Dobra rozumiem przecież moduł=√a2+b2 we wzorze
16 lis 17:51
Sys: Z tym przekształceniem domyślam się, że będzie to okrąg z zakreskowanym polem wewnątrz,
nie wiem tylko jak dojść do tej postaci
16 lis 18:13
PW: Wykonujemy rachunki nie wymnażając (b+1)2:
a4 − 2a2(b+1)2 + (b+1)4 + 4a2(b+1)2 < 81
a4 + 2a2(b+1)2 + (b+1)4 < 81
i znowu lewa strona "się zwija":
(a2 + (b+1)2)2 < 81
16 lis 18:27
Sys:
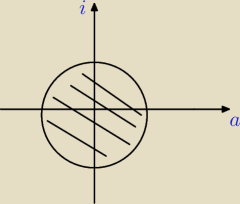
No i teraz wszystko jasne, niepotrzebnie wymnożyłem przez to (b+1)
2, wtedy bym już zauważył.
Rozwiązaniem są liczby znajdujące się wewnątrz okręgu S=(0,−1) o promieniu 9 bez krawędzi
zewnętrznych.
Dobrze zaznaczyłem na wykresie podpisy osi?
16 lis 18:39
 No i teraz wszystko jasne, niepotrzebnie wymnożyłem przez to (b+1)2, wtedy bym już zauważył.
Rozwiązaniem są liczby znajdujące się wewnątrz okręgu S=(0,−1) o promieniu 9 bez krawędzi
zewnętrznych.
Dobrze zaznaczyłem na wykresie podpisy osi?
No i teraz wszystko jasne, niepotrzebnie wymnożyłem przez to (b+1)2, wtedy bym już zauważył.
Rozwiązaniem są liczby znajdujące się wewnątrz okręgu S=(0,−1) o promieniu 9 bez krawędzi
zewnętrznych.
Dobrze zaznaczyłem na wykresie podpisy osi?