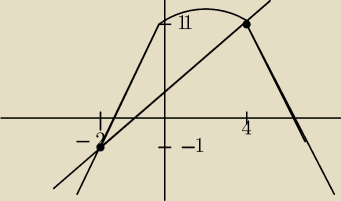
Pole Asia: Witam, proszę o wytłumaczenie skąd wzięło się to co jest zaznaczone na czerwono. Oblicz pole. y = 2x + 3 y = −x² + 4x + 11 2x + 3 = − x² + 11 x² − 2x + 3 − 11 = 0 x² − 2x −8 = 0 Δ= b² − 4ac Δ= (−2)² − 4 * 1 * (−8) Δ= 36 √Δ = 6 x₁ = −2 x₂ = 4 y₁ = −1 y₂ = 11 ∫⁴ −2 [−x² + 4x + 11 − 2x − 3]dx= ∫⁴ −2 (−x² + 2x + 8)dx= −¹₃x³ |⁴|₋2 +2 * ¹₂x² |⁴₋2 + 8x |⁴₋2 = −¹₃ (64+8) + 1(16−4)+8(4+2)= − 24 + 12 +48 = 60 − 24 + 36 [j²}

Asia: ∫ na górze 4, a na dole −2 nie wiedziałam jak zrobić

Asia: Pomocy

jo: Jeśli funkcje f i g są ciągłe w przedziale <a,b> i f(x)≤g(x) w tym przedziale, to pole obszaru ograniczonego wykresami tych funkcji i prostymi x=a i x=b jest równe: Pole = ∫^b_a (g(x) − f(x)) dx

jo: Widać już z tego twierdzenia dlaczego tak?

Asia: No dobra, to wiem. ale skąd się wzięło np. −¹₃x³ ∫⁴₋₂ ... i reszta do końca

Asia:

Asia: Hallo, pomoże ktoś

Asia: Dziękuje bardzo, sama zdążyłam do tego dojść1