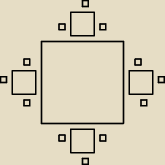
Szereg geometryczny-zadania Stooley: 7.193. Budujemy nieskończony ciąg figur (F_n). Pierwszą figurą jest kwadrat o boku a. Następnie dzielimy każdy bok kwadratu na trzy różne części i "doklejamy" cztery kwadraty o boku a/3. W ten sposób otrzymujemy drugi wyraz ciągu. W kolejnym kroku dzielimy trzy boki mniejszych czterych kwadratów i "doklejamy" do nich dwanaście kwadracików o boku a/9. Analogicznie konstruujemy kolejne figury. b) Oblicz lim_n→∞L_n i lim_n→∞P_n Dla ułatwienia: ZADANIE POCHODZI ZE ZBIORU ZADAŃ DLA LICEUM I TECHNIKUM ZAKRESU ROZSZERZONEGO CZĘŚĆ DRUGA AUTORSTWA MARCINA KURCZABA, ELŻBIETY KURCZAB I ELŻBIETY ŚWIDY.

Adamm: L₁=4a

	a
L2=4a+4*3*
	3

	a		a
L3=4a+4*3*		+4*3*3*
	3		9

	a		a		a
Ln=4a+4*3*		+4*3*3*		+...+4*3n−1*
	3		9		3n−1

L_n=4(a+a+a+...+a)=4*n*a lim L_n = ∞ P₁=a²

	a
P2=a2+4*(		)2
	3

	a		a
P3=a2+4*(		)2+4*3*(		)2
	3		9

	a		a
Pn=a2+4*(		)2+...+4*3n−2(		)2
	3		3n−1

	a		a2
Pn=a2+4*(		)2+...+4*
	3		3n

	a		a2		1		1
4*(		)2+...+4*		=4a2(		+...+		)=
	3		3n		9		3n

	1		1   1−( )n−1   3		1
=4a2*		*		=2a2(1−(		)n−1)
	3		1   1−   3		3

lim P_n = 2a²

Adamm:

	1		1		1		1   1−( )n−1   3
pomyłka, 4a2(		+...+		)=4a2*		*		=
	9		3n		9		1   1−   3

	2		1
=		a2*(1−(		)n−1)
	3		3

	2		1
Pn=a2+		a2*(1−(		)n−1)
	3		3

	2		5
lim Pn = a2+		a2=		a2
	3		3