Analiza - Optymalizacja Sonic: Muszę znaleźć trójkąt prostokątny o największym polu, o przeciwprostokątnej 10 cm. Zatrzymałem się na momencie liczenia P(x) − pola od x. Jak w łatwy sposób poradzić sobie z pochodną tego pola? P(x)=√100−x²*0,5*x P'(x)= ?

zef: 0,5x√100−x²=0,5x*[(10−x)(10+x)]^0,5= √0,25x²(10−x)(10+x) Tak chyba można zwinąć

Jack: "Włóż" ten x co jest za pierwiastkiem pod pierwiastek a nastepnie funkcje pod pierwiastkiem nazwij sobie np. f gdyz bedzie przyjmowac max dla tych samych argumentow co pierwiastek. Jesli napisalem nieczytelbie No to chodzi mi : P(x) = √x²(100−x²)*1/2 f(x) =x²(100−x²) = 100x² − x⁴ I policz pochodna funkcji f oraz max dla f.

Sonic: Zwinięcie zauważyłem, ale nic mi ono nie dało, nadal nie mam pojęcia jak zastosować na nim wzory...

Sonic: Dzięki wielkie Jack. O to chodziło!

PW: Nadmiar wiedzy bywa szkodliwy. Narysować w półkolu trójąt prostokątny (przeciwprostokątna jest średnicą, wierzchołek kata prostego leży na półokręgu). Kiedy pole jest największe? Wtedy, gdy największa jest wysokość opuszczona na przeciwprostokątną, to znaczy gdy wysokość jest równa promieniowi.

Sonic: PW genialne Mam nadzieję, że trafię na tego typu zadanie na sprawdzianie i zastosuję ten sposób.

PW: Nie "genialne", ale "gimnazjalne"

Sonic: A jak myślisz PW, czy jak opiszę to w ten sposób co Ty, to dostanę maksymalną liczbę punktów za zadanie, czy trzeba coś jeszcze dopisać?

Sonic: Niby gimnazjalne, ale zastanawiam się, czy przez wzgląd na to, że przerabialiśmy pochodne funkcji nie będę zmuszony do liczenia tego tym dłuższym sposobem...

PW: To zależy od sformułowania zadania. Jeżeli nie będzie "stosując rachunek różniczkowy", tylko tak jak podałeś, to stawiam piątkę temu, kto się najmniej narobi − najlepsze są rozwiązania elementarne.

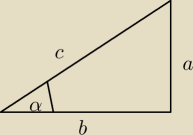
PW: Lepszy sposób − jeżeli już musisz rozwiązywać stosując pochodne − polega na wybraniu jako

	π
zmiennej kąta α, α∊(0,		)
	2

	1		1		1		1
P(α) =		ab =		c.sinα.c.cosα =		c2(2sinαcosα) =		c2sin(2α)
	2		2		4		4

	c2		c2
P'(α) =		cos(2α).2 =		cos(2α)
	4		2

	π
P'(α) = 0 ⇔ cos(2α) = 0, α∊(0,		)
	2

	π		π
P'(α) = 0 ⇔ 2α =		⇔ α =
	2		4

Pokazać, że rzeczywiście jest to punkt, w którym P(α) osiąga maksimum i mamy odpowiedź: trójkąt musi mieć oba kąty ostre równe, czyli musi być równoramienny. Kawał dobrej (?) roboty i mamy to samo co gimnazjalista.