| π | ||
Wykaż, że dla każdej liczby x∊(0; | ) prawdziwa jest podana nierówność: | |
| 2 |
proszę o pomoc
| 1 | 1 | |||
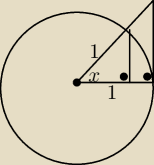
pole małego trójkąta − | sinx, pole całego wycinka − | *x, pole dużego − | ||
| 2 | 2 |
| 1 | ||
− | tgx | |
| 2 |
| π | ||
więc mamy sinx<x<tgx dla 0<x< | ||
| 2 |
chociaż myślałam, że to zadanie jest łatwiejsze xd