pole trójkąta
Adamm: wzór na pole trójkąta dla danych 3 punktów A=(a1, a2, a3), B=(b1, b2, b3),
C=(c1, c2, c3)
czy jest na to wzór z użyciem wyznaczników?
12 lis 23:04
Janek191:
→ →
P = 0,5*I det ( AB , AC ) I
12 lis 23:06
Janek191:
W I wierszu pewnie będą jedynki.
12 lis 23:07
Adamm: dziękuję

12 lis 23:09
Krzysiek:
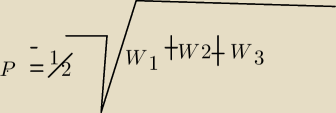
Trzy wyznaczniki
|1 x
1 y
1|
2
|1 x
2 y
2|
|1 x
3 y
3|
|1 x
1z
1|
2
|1 x
2 z
2|
|1 x
3 z
3|
|1 y
1 z
1|
2
|1 y
2z
2|
|1 y
3z
3|
| | 1 | |
Pod pierwiastkiem stopnia drugiego dodajesz te wykadniki i mnozysz przez |
| |
| | 2 | |
12 lis 23:17
Adamm: również dziękuję
12 lis 23:21
Krzysiek: Zapomnialem Ci napisac ze ten wzor jest w ksiazce
Marceli Stark Geometria analityczna z ewstepem do geometrii wielowymiarowej
Biblioteka Matematyczna Tom 17 . (wydanie 6 1974r mam .
12 lis 23:24
jc:
u + B−A, v = C−A
P = 1/2 *
| u*u u*v |1/2
| v*u v*v |
12 lis 23:24
'Leszek: Pole trojkata ktorego boki sa wektorami AB i AC jest liczbowo rowne polowie iloczynu
wektorowego wektorow AB i i AC ,czyli jest to polowa dlugosci wektora ,ktory otrzymujemy
jako iloczyn wektorowy wektorow AB i AC , a to nie jest wartosc wyznacznika .
12 lis 23:27
'Leszek: Wzor podany przez p.Janek191 dotyczy plaszczyzny R2 a nie dotyczy R3 .
12 lis 23:34
jc: A jednak jest to połowa z pierwiasteka z pewnego wyznacznika, jak powyżej napisałem.
Wzór działa w przestrzeni dowolnego wymiaru i ma oczywiste uogólnienie.
12 lis 23:34
'Leszek: Wynikiem iloczynu wektorowego dwoch wektorow jest wektor , a wyznacznik macierzy
kwadratowej jest skalarem .Wspolrzedne tego wektora obliczamy stosujac wyznaczniki
i tylko tyle.
12 lis 23:38
Adamm: dziękuję za kolejny wzór
'Leszek, R2? ze źródeł z których korzystam wynika że ta zależność działa również dla R3
możesz to bardziej rozjaśnić?
12 lis 23:42
jc: Wzór który podałem działa w przestrzeni dowolnego wymiaru.
pole równoległoboku rozpiętego na wektorach u i v =
| u*u u*v |1/2
| v*u v*v |
* oznacza iloczyn skalarny
12 lis 23:50
'Leszek: Dane sa wierzcholki trojkata
A(1,2,3)
B(2,3,−4)
C(−2,4,5)
Tworzymy wektory
AB = [1,1,−7]
AC= [−3,2,2]
Obliczamy iloczyn wektorowy AB x AC = i*(1*2+7*2) − j*(1*2− 3*7) +k*(1*2+1*3)
Gdzie i ,j ,k sa to wersory
Czyli AB x AC = 16*i + 19*j + 5*k
Dlugosc tego wektora |AB xAC| = √162 + 192 + 52
13 lis 00:04
jc:
AB*AB = 51
AC*AC = 17
AB*AC = −15
| 51 −15 |
| −15 17 | = 642
13 lis 00:15
Adamm: próbowałem zrobić to metodą którą podał
Krzysiek jednak wynik wychodzi inny,
13 lis 00:41
Adamm: nieważne, nie było tematu
13 lis 00:43

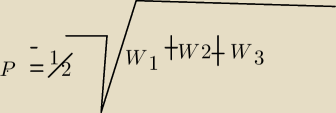 Trzy wyznaczniki
|1 x1 y1|2
|1 x2 y2|
|1 x3 y3|
|1 x1z1|2
|1 x2 z2|
|1 x3 z3|
|1 y1 z1|2
|1 y2z2|
|1 y3z3|
Trzy wyznaczniki
|1 x1 y1|2
|1 x2 y2|
|1 x3 y3|
|1 x1z1|2
|1 x2 z2|
|1 x3 z3|
|1 y1 z1|2
|1 y2z2|
|1 y3z3|