Równoległobok
LHC: Udowodnij, że w równoległoboku ABCD
AB2 + BC2 + CD2 + DA2 = AC2 + BD2
12 lis 21:42
Eta:
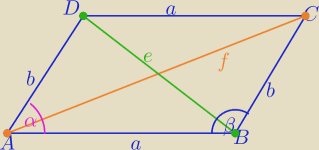
W każdym równoległoboku zachodzi równość : ( wykaż z twierdzenia kosinusów
f
2+e
2=2a
2+2b
2
co daje tezę : |AC|
2+|BD|
2= |AB|
2+|CD|
2+|AD|
2+|BC|
2
12 lis 21:53
Benny: 
12 lis 22:22
Eta:
12 lis 22:43
LHC: Yyy
12 lis 23:10
Jack: Dostales ladne rozw. i nie czaisz?...
Przede wszystkim α = 180 − β (mam nadzieje ze to jasne, jesli nie, napisz (1))
z tw. cos w trojkacie ABC (jesli nie jasne pisz (2))
f2 = a2 + b2 − 2ab cos β
z tw. cos w trojkacie BCD (jesli nie jasne pisz (3))
e2 = a2 + b2 − 2ab cosα
jednakze cos α = cos(180 − β) = − cos β, (jesli nie jasne pisz (4)), zatem
e2 = a2 + b2 + 2ab cos β
czyli e2+f2 = a2+b2−2abcosβ + a2+b2 + 2abcosβ = 2a2+2b2
12 lis 23:36
Eta:
12 lis 23:37
LHC: Wszystko rozumiem, a można innym sposobem? Beż użycia twierdzenia cosinusów
12 lis 23:44
Jack: w ktorej jestes klasie / nie miales tw. cosinusow ani sinusow?
12 lis 23:49
LHC: W drugiej, jeszcze nie miałem
12 lis 23:50
Benny: Z twierdzenia Pitagorasa można.
12 lis 23:54
Benny:
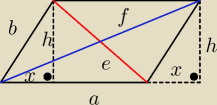
f
2=(a+x)
2+h
2
e
2=h
2+(a−x)
2
b
2=x
2+h
2
h
2=b
2−x
2
f
2=(a+x)
2+b
2−x
2
e
2=b
2−x
2+(a−x)
2 dodaje stronami
f
2+e
2=2b
2−2x
2+2a
2+2x
2
f
2+e
2=2a
2+2b
2
_________________
12 lis 23:58
Jack: Benny
13 lis 00:00
Benny: 
13 lis 00:13
Krzysiek: Dziękuję
13 lis 00:15