Proszę o sprawdzenie JAck: Proszę o sprawdzenie poprawności rozwiązania, zapisu itd, niedługo mam kolokwium. Wykazać że funkcja posiada odwrotną i wyznaczyć ją f(x)=(1+x)/(1−x). zał: x∊R/{1} y=(1+x)/(1−x)=^−2x_(x−1)+1→funkcja jest rosnąca w całej swojej dziedzinie oraz f:R/{1}→R⇒czyli jest "na", więc istniej do niej funkcja odwrotna taka że f⁻1(x):R→R/{1} y=(1+x)/(1−x) y−xy=1+x y−1=x(1+y) x=(y−1)/(1+y) ⇒y= f⁻1(x)=(x−1)/(x+1)

Adamm: jaki jest zbiór wartości funkcji f(x)? bo nie jest to zbiór rzeczywistych

Janek191:

	1 + x
y =		x ≠ 1
	1 − x

y − y x = 1 + x x + y x = y − 1 x*( 1 + y) = y − 1

	y − 1
x =
	y + 1

Po zamianie zmiennych

	x − 1
y =		x ≠ − 1
	x + 1

Jest ok g = f⁻¹

JAck: racja, ma asymptotę poziomą w y=−1, czyli nie może być "na" czyli nie ma odwrotnej tak?

JAck: Zw∊R/{−1} czyli ona dalej będzie "na" bo f:R/{1}→R/{−1}, więc f−1(x):R{−1}→R/{1}, Czy dobrze myślę?

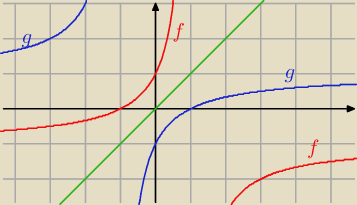
Janek191: Patrz na rysunek − wykresy są symetryczne względem prostej y = x.

JAck: Widzę, że są symetryczne względem y=x. Dobra bo ja myślałem ze jak jest "na" to Zw∊R ,ale tak nie jest, Zw to wartości funkcji.