logikq
kotek: (A ∩ C) \ [ (A \ B ) ∩ ( C \ B )]
Sprowadzic do najprostszej postaci
12 lis 17:10
Adamm: (A\B)∩(C\B)=(A∩C)\B
(A∩C)\((A∩C)\B)=A∩B∩C
12 lis 17:16
kotek: a taki przykład:
[(A∩B) \ (C\B)] ' ?
12 lis 17:24
Adamm: A∩B
12 lis 17:29
Adamm:
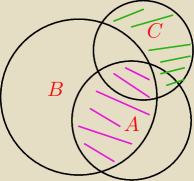
zielony to C\B, fioletowy to A∩B, nie ma czego odejmować od zbioru A∩B bo
(A∩B)∩(C\B)=∅
12 lis 17:33
kotek: czyli znak ' nic nie zmienia?
12 lis 17:35
Adamm: nie widziałem tego dopełnienia, ale zależy na jakim uniwersum pracujemy
12 lis 17:37
Adamm: w każdym razie (A∩B)'
12 lis 17:37
kotek: ?
12 lis 18:20
Adamm: (A∩B)'=U\(A∩B) i można tak zostawić, bo prościej nie będzie
12 lis 18:22
Tomasz: Adamm a co Ty na ten przykład? Siedze juz nad nim sporo czasu:
X\{(A\C)∪[(A∩B)\C]} ' dopełnienie całego tego nawiasu klamrowego
12 lis 18:37
Adamm: [(A∩B)\C]⊂(A\C) stąd [(A∩B)\C]∪(A\C) = A\C
czyli X\{A\C}'
X jest uniwersum? jeśli tak to po prostu
A\C i można zostawić
12 lis 18:42
Tomasz: a jesli nie?
12 lis 18:44
Adamm: jeśli nie to zapis taki raczej może zostać, bo prostszego nie będzie
12 lis 18:45
Kotek: napisałes: (A\B)∩(C\B)=(A∩C)\B
(A∩C)\((A∩C)\B)=A∩B∩C
ale nie rozumiem ostatniego znaku równosci
12 lis 18:49
Tomasz: dziękuje
12 lis 18:49
Adamm:
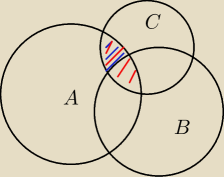
niebieski to (A∩B)\B, czerwony to A∩C
zabierz zbiór niebieski od czerwonego, będziesz miał A∩B∩C
12 lis 18:52
Adamm: (A∩C)\B
12 lis 18:52
Kotek: skoro z A∩C wyrzucamy B to zostaje nam A∩C, a u Ciebie zostało B
12 lis 18:52
Kotek: aaa
12 lis 18:53
Kotek: dziękuje
12 lis 18:53
Adamm: 
głupoty gadasz
12 lis 18:54
Kotek: masz racje , gadam głupoty.. jak sobie to narysowałam to do tego doszłam
12 lis 18:56