Nierownosci wielomianowe
Alina: Rozwiąż nierownosc
Proszę o pomoc wraz z tlumaczeniem dlaczego tak.
1) 5|x|+2|x|3≥0
2) |x4−9x2|>x4−9x2
Jeszcze cos z rozkladu wielomianow na czynniki:
3) W(x)= x12−2x6+1
4) W(x)= 4x4−12x3+25x2−48x+36 (czy ten przyklad musi byc robiony schematem hornera?)
Tutaj przede wszystkim chcialbym poznac jakis sposob na szybkie dostrzeganie par.
10 sty 21:30
Alina: Prosze o Pomoc
10 sty 21:48
Alina: 
10 sty 22:06
Alina: Potrzebne mi to na jutro− prosze o pomoc
10 sty 22:31
ula: 1/
{5x+2x3≥0 dla x≥0
{−5x−2x3≥0 dla x<0
x(5+2x2)≥0 (to co w nawiasie jest zawsze +)
x≥0
−x(5+2x2)≥0 (to co w nawiasie jest zawsze +)
x<0
Odp. x∊R
10 sty 22:33
Alina: Dzieki, a pozostale?
10 sty 22:45
ula:
2/
1/x
4−9x
2>x
4−9x
2 dla x
4−9x
2≥0
x∊zb. pusty x
2(x
2−9)≥0
x
2(x−3)(x+3)≥0
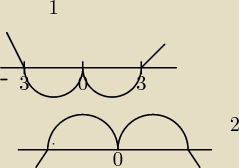
rys. 1 to dziedzina x∊(−∞,−3>u<3;∞)
2/ −x
4+9x
2>x
4−9x
2 dla x
4−9x
2<0
−x
2(x
2−9)>0 x∊(−3,3)− {0}
rys. 2 x∊(−3;3) −{0} dla x∊(−3,3)− {0}
10 sty 22:49
ula: 4 najprościej schematem
nie ma szybkiego sposobu wyszukiwania dzielnika
trzeba podstawiać i już
w 4 przykladzie trzeba sprawdzić {+−1,+−2.+−3, +−6.....}
w 3 nie pomyliłaś nigdzie znaków? jeśli tak to można x6=t
10 sty 22:56
Alina: 3) x12 −2x6+1
10 sty 22:58
Alina: w 4 przykladzie trzeba sprawdzić {+−1,+−2.+−3, +−6.....} − skad to wiesz? Wypisujesz po
prostu dzielniki 36?
10 sty 22:59
Anna:
3) W(x) = x12 − 2x6 + 1 = x12 − x6 − x6 + 1 = x6(x6 − 1) − (x6 − 1) =
= (x6 − 1)(x6 − 1) = (x6 − 1)2 = [(x2 − 1)(x2 + x2 + 1)]2 =
= (x2 − 1)2(2x2 + 1)2
10 sty 23:00
Alina: OK, rozumiem, Dziekuje
10 sty 23:16
Anna: 
10 sty 23:32