Stereometria Kwerti : Prostopadłościan ABCDA1B1C1D1 przecięto płaszczyzną nierównoległą do podstawy ABCD. Ta płaszczyzna przecięła prawędzie boczbe AA1, BB1, CC1, DD1 odpowiednio w punktach A2, B2, C2, D2. Wykaż, że: a) czworokąt A2B2C2D2 jest równoległobokiem b) |AA2|+|CC2|=|BB2|+|DD2|

Kwerti : UP

Kwerti: UP

===: a wkład własny ... przyzwoity rysunek chociażby Wrzuciłeś zadanko (w sumie fajne) i tylko sprawdzasz co kilka godzin czy ktoś zrobił wszystko za Ciebie

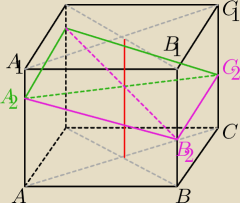
===: z tego już coś widać A dalej zrób przekroje po przekątnych podstaw

===: Na przekrojach zauważ, że trapezy ACC₂A₂ oraz BDD₂B₂ mają taką samą średnią podstaw ... i tyle podpowiedzi

Kwerti : Tyle to i ja wiem, rysunek też nie problem. Tylko mi chodzi żeby to wszystko tak zapisać żeby zgadzało się z kluczem.

===: Dobre sobie ... to opisuj ... czego nie rozumiesz Przekrojów po przekątnych też nie zrobiłeś a na nich jest wszystko. Przy takim podejściu dalej nie pomogę.

Krzysiek: Przy takim podejsciu tylko duch puszczy został

===: ... ogarniesz to? "tyle to i on wie... ale chodzi o to aby to tak opisać aby zgadzało się z kluczem" A ja nie wiem czemu myślałem, że on chce czegokolwiek się nauczyć. A to tylko ma się zgadzać z kluczem.

Kwerti : Oczywiście, że chce się nauczyć nie po robię co dzień tyle zadań. Chodzi mi, że nie rozumiem tego zadania. Mógłby Pan jeszcze naprowadzić?

===: Z treści zadania wynika, że płaszczyzna nie równoległa do podstawy przecina wszystkie krawędzie boczne. Do tej płaszczyzny należą wszystkie jej "ślady" na ścianach bocznych. Zauważ, że A₂B₂ i C₂D₂ leżą na tej płaszczyźnie ale nie przecinają się bo należą jednocześnie do płaszczyzn, które są w stosunku do siebie równoległe (przeciwległe ściany prostopadłościanu). Oczywistym więc jest że odcinki te są w stosunku do siebie równoległe, Czworokąt którego boki są parami równoległe to równległobok ... i to jest podpunkt a) Twego zadania.

Kwerti : Dziękuję, rozumiem. To pkt a) to opisowe, myślałem że na literach trzeba to uzasadniać. A podpowiedz do pkt b mogę prosić?

===: zobaczysz jak narysujesz przekroje ... przecież rysunek to nie problem

Kwerti : Mam, dwa trapezy i mają te samą średnią podstaw. https://matematykaszkolna.pl/forum/336064.html możesz zobaczyć na to, też fajne zadanie pkt a) zrobiłem i nie wiem jak b)