Stereometria
Kwerti : Dany jest ostrosłup ABCD, w którym krawędzie AD, BD, CD są parami prostopadłe. Pola ścian
bocznych ABD, BCD, ACD są odpowiednio równe P1, P2, P3. Wykaż, że objętość V ostrosłupa ABCD
jest równa (√2P1*P2*P3)/3.
Proszę również o wytłumaczenie co znaczy parami prostopadłe i czym się to charakteryzuje.
12 lis 13:35
Eta:
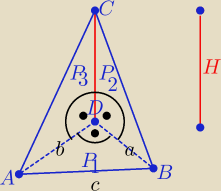
| | 2P3 | |
P(ADC)=2P3=H*b ⇒ H= |
| |
| | b | |
| | 2P2 | |
P(BCD)=2P2= H*a ⇒ H= |
| |
| | a | |
| | 2P1 | |
P(ABD)= 2P1 = a*b ⇒ a= |
| |
| | b | |
to :
| | 2P2*b | | P2*b | | 2P3 | |
H= |
| = |
| i b= |
| |
| | 2P1 | | P1 | | H | |
| | 1 | | √2P1*P2*P3 | |
V= |
| P1*H = |
| |
| | 3 | | 3 | |
12 lis 14:23
