unkt B = (-3,3) jest jednym z wierzchołków prostokąta ABCD. Wierzchołek D tego p Olx: Punkt B = (−3,3) jest jednym z wierzchołków prostokąta ABCD. Wierzchołek D tego prostokąta należy do prostej o równaniu 7x − 4y + 33 = 0. Wektor AD = [−2,4]. Napisz równania przekątnych tego prostokąta. W odpowiedzi jest: 7x − 4y + 3 = 0 i x + 8y − 21 Robię to zadanie od kilku godzin i wychodzą mi inne wyniki. Czy te odpowiedzi są poprawne czy może jednak jest błąd?

Janek191: Jest błąd w zadaniu, bo B i D nie mogą leżeć na jednej prostej,

Adamm: wyznaczasz punkt C, bo wektor AD jest taki sam jak BC, następnie możesz wyliczyć prostą prostopadłą przechodzącą przez punkt C, czyli −2x+4y+c=0 a c wyliczasz z faktu że przechodzi przez C, dalej możesz obliczyć punkt D jako przecięcie się dwóch prostych, a punkt A z wektora AD, i liczysz dwie proste − przekątne

Adamm: Janek191 mogą

Janek191: Wróć − może BD to przekątna prostokąta : 7 x − 4 y + 33 = 0

Olx: No właśnie mi wyszło że 7x − 4y + 33 = 0, tylko nie zgadza się to z odpowiedzią.

Adamm: może ktoś zgubił liczbę, musi być dobrze, no chyba że punkty B i D są tymi samymi

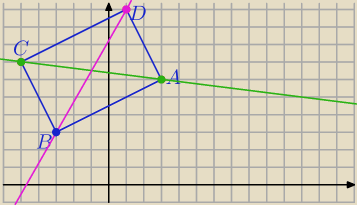
Eta: A(3,6) , B(−3,3) , C(−5,7) , D(1,10) Prawidłowa Odp: przekątne mają równania: BD: 7x−4y+33=0 −−− była dana już w treści zadania bo i D i B(−3,3) ∊(7x−4y+33=0) AC: x+8y−51=0