rozwiąż nierówność:
JAck:
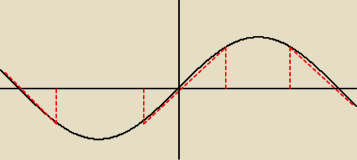
rozwiąż nierówność:
|sinx|sinx≤1/2 zał: x∊R ⋀ |sinx|≥0
dla sinx≥0
sin
2x≤1/2
|sinx|≤
√2/2
sinx≤
√2/2 ⋀ sinx≥−
√2/2
dla sinx≤0
sin
2x≥−1/2
nierównośc spełniona dla x∊R
wyszły mi przedziały odczytane z wykresu x∊<−π/4+2kπ; π/4+2kπ>∪ <3/4π+ 2kπ; 5/4π+2kπ> k∊Z,
ale w odpowiedziach jest x∊<2kπ; π/4+2kπ>∪ <3/4π+2kπ; π+2kπ>∪ <π+2kπ; 2π+2kπ> k∊Z.
Gdzie jest błąd? Nie mam możliwości odpowiadania, więc proszę o jasną odpowiedź. Dziękuje.
11 lis 20:22
PW: Druga nierówność to
| | 1 | |
sin2x ≥ − |
| , x∊(−π, 0) |
| | 2 | |
Jej rozwiązaniem są wszystkie x z rozpatrywanego przedziału, nie wolno pisać "x∊R".
Dlatego w odpowiedzi są przedziały (−π + 2kπ, 0 + 2kπ), które równie dobrze można zapisać jako
(π + 2mπ, 2π + 2mπ),
czyli tak jak w książce. Korzystali z rysunku dla przedziału [0, 2π), a Ty korzystasz z rysunku
dla przedziału (−π, π>, stąd różne
podstawowe rozwiązania przesuwane o wielokrotność
okresu..
11 lis 22:18
JAck: jaki znak logiczny powinien stać pomiędzy dwoma nierównościami? w sensie między sinx≥0,a
sinx≤0

?
12 lis 16:44
PW:
sinx ≥ 0 ∧ sinx ≤ 0
to tylko takie punkty, dla których sinx =0.
Masz rozwiązać nierówność dla wszystkich x, a więc badasz osobno
sinx ≥ 0 ∨ sinx ≤ 0.
W Twoim rozwiązaniu otrzymujesz dwie nierówności połączone spójnikiem "lub", a więc rozwiązanie
jest sumą rozwiązań.
Nie wiem dokładnie jakie masz wątpliwości, ale zwracam uwagę, że w 5. linijce rozwiązania z
20:22 jest błąd:
z
przy założeniu sinx > 0 wynika tylko
12 lis 17:09
 rozwiąż nierówność:
|sinx|sinx≤1/2 zał: x∊R ⋀ |sinx|≥0
dla sinx≥0
sin2x≤1/2
|sinx|≤√2/2
sinx≤√2/2 ⋀ sinx≥−√2/2
dla sinx≤0
sin2x≥−1/2
nierównośc spełniona dla x∊R
wyszły mi przedziały odczytane z wykresu x∊<−π/4+2kπ; π/4+2kπ>∪ <3/4π+ 2kπ; 5/4π+2kπ> k∊Z,
ale w odpowiedziach jest x∊<2kπ; π/4+2kπ>∪ <3/4π+2kπ; π+2kπ>∪ <π+2kπ; 2π+2kπ> k∊Z.
Gdzie jest błąd? Nie mam możliwości odpowiadania, więc proszę o jasną odpowiedź. Dziękuje.
rozwiąż nierówność:
|sinx|sinx≤1/2 zał: x∊R ⋀ |sinx|≥0
dla sinx≥0
sin2x≤1/2
|sinx|≤√2/2
sinx≤√2/2 ⋀ sinx≥−√2/2
dla sinx≤0
sin2x≥−1/2
nierównośc spełniona dla x∊R
wyszły mi przedziały odczytane z wykresu x∊<−π/4+2kπ; π/4+2kπ>∪ <3/4π+ 2kπ; 5/4π+2kπ> k∊Z,
ale w odpowiedziach jest x∊<2kπ; π/4+2kπ>∪ <3/4π+2kπ; π+2kπ>∪ <π+2kπ; 2π+2kπ> k∊Z.
Gdzie jest błąd? Nie mam możliwości odpowiadania, więc proszę o jasną odpowiedź. Dziękuje.
 ?
?