trójkąt Tomek: W trójkącie ABC na boku BC obrano punkt M tak że |MC|=2|CB| i na boku AC obrano punkt N tak że |AN|=3|NC| proste AM i BN przecinają się w punkcie K Wiedząc,że pole trójkąta KMB jest równe 14 i prosta CK przecina bok AB w punkcie L a) oblicz pole trójkąta ABC b) stosunek |CK| : |KL| Proszę o pomoc

Jack: tożto bez sensu (pierwsze zdanie)

Tomek: przepraszam |MC|=2|MB|

Bartek: przede wszystkim dobry rysunek

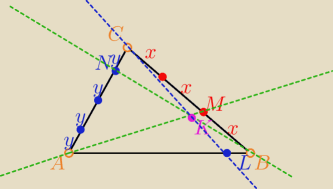
Jack: Teraz lepiej PS rysunek "mniej wiecej"

Bogdan:

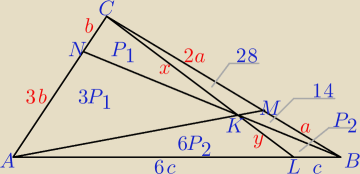
	a		b		|AL|		|AL|		6
Z twierdzenia Cevy:		*		*		= 1 /*6 ⇒		=
	2a		3b		|LB|		|LB|		1

Pola P_ALC = 6P_LBC ⇒ 4P₁ + 6P₂ = 6(P₂ + 42} ⇒ P₁ = 63 Pola P_MCA = 2P_MAB ⇒ 28 + 4P₁ = 2(14 + 7P₂) ⇒ 28 + 4*63 = 28 + 14P₂ P₂ = 18 Pole P_ABC = 4P₁ + 7P₂ + 42 = ... h − długość wysokości trójkąta KCA opadająca na bok KC (ozn. x) i jednocześnie długość wysokości trójkata LKA opadająca na bok LK (ozn. y)

	1		1
Pola trójkątów: PKCA =		xh = 4P1 = 4*63 i PLKA =		yh = 6P2 = 6*18
	2		2

PKCA		1   xh 2		4*63		x		|CK|
	=		=		=		=
PLKA		1   yh 2		6*18		y		|KL|

|CK|
	= ...
|KL|