Tryg zef: Czy mając równanie: mam równanie: sinx+cosx=√2 podniosę to do kwadratu stronami sin²x+cos²x+2sinxcosx=2

	1
sinxcosx=		, z równania głównego wiem też że sinx+cosx=√2, sinx=√2−cosx to podstawię.
	2

	1
(√2−cosx)cosx=
	2

	1
√2cosx−cos2x−		=0
	2

niech t=cosx

	1
√2t2−t−		=0
	2

	√2
(t−		)2=0
	2

	√2
t=
	2

	√2
cosx=
	2

	π		3π
x1=		+2kπ lub x2=		+2kπ
	4		4

A w odpowiedzi uwzględnione jest tylko x₁ może mi ktoś wytłumaczyć dlaczego ? Zauważyłem że

	1
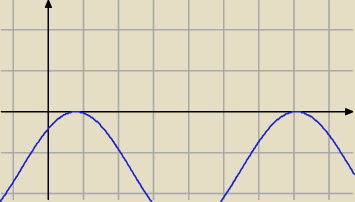
wykres funkcji f(x)=√2cosx−cos2x−		ma dziedzinę x∊<0;∞) jednak nie wiem skąd to
	2

wynika, może mi ktoś wytłumaczyć ?

Janek191: sin x + cos x = √2 ⇒ cos x = √2 − sin x sin² x + cos² x = 1 więc sin² x + ( √2 − sin x)² = 1 sin² x + 2 − 2√2 sin x + sin² x = 1 2 sin² x − 2√2 sin x + 1 = 0 Δ = 8 − 4*2* 1 = 0

	2√2		√2
sin x=		=
	4		2

	π
x =		+ 2π*k k − dowolna liczba całkowita
	4

zef: no i mając

	√2
sinx=
	2

Czemu mamy tylko 1 rozwiązanie ? Przecież na ogół to:

	π		π		3π
x=		+2kπ i 2 rozwiązanie x=π−		+2kπ=		+2kπ czemu tego drugiego nie ma ?
	4		4		4

Mila: sinx+cosx=√2 / :√2

√2		√2
	*sinx+		*cosx=1
2		2

	π		π
cos		*sinx+sin		*cosx=1⇔
	4		4

	π
sin(x+		)=1⇔
	4

	π		π
x+		=		+2kπ
	4		2

	π
x=		+2kπ , k∊C
	4

zef: Dziękuje Mila, też nad tym sposobem rozwiązania myślałem, ale dalej się zastanawiam co jest nie tak w tym co ja zrobiłem. Czemu ujemne rozwiązania się nie liczą

Mila: 1) Jeżeli podnosisz do kwadratu wyrażenie algebraiczne to mogą się pojawiać tzw. pierwiastki obce. Bezpiecznie jest podnosić do kwadratu wyrażenie nieujemne. Sprawdzamy:

	π
x=
	4

	π		π		√2		√2
L=sin		+cos		=		+		=√2=P
	4		4		2		2

	3π
x=
	4

	√2		√2
L=		−		=0≠P
	2		2

Twoje nowe równanie nie jest równoważne z wyjściowym.

	√2
2) Równanie cosx=		źle rozwiązałeś
	2

	π		π		π
x1=		+2kπ lub x2 =−		+2kπ (albo x2=2π−		+2kπ)
	4		4		4

Już to chyba Ci tłumaczyliśmy z PW ( a może komu innemu?)

zef:

	√2
Tak, tak z tym cosx=		to już taki błąd bo na szybko pisałem i pomyślałem o sinusie. 2)
	2

wszystko jest zrozumiałe. Ale o pierwiastkach obcych pierwszy raz słyszę, postaram się unikać podnoszenia do kwadratu, dziękuję bardzo !

Mila: