Wykres Agata: Naszkicuj wykres funkcji: a) f(x) = |x−3|(x−1) b) f(x)=(x+1)|x−2| c) f(x) = x|x+1| − x c) f(x) = x² + 4|1−x| dla xe (0,2> Prosze o wytlumaczenie szczegolowe jak to robic

Adamm: dzielisz na przedziały i lecisz, np. f(x)=x|x+1|−x dla x<−1, f(x)=−x²−2x, rysujesz dla danego przedziału dla x≥−1, f(x)=x², to samo

Agata: nie czaje

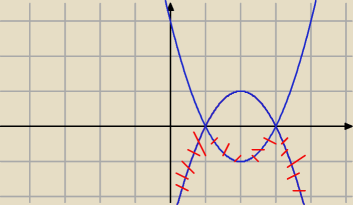
PW: Dla zadań a) i b) widzę możliwość wykręcenia się sianem. f(x) = |x−3|(x−1) ⇒ f²(x) = |x−3|²(x−1)² = (x−3)²(x−1)² = [(x−3)(x−1)]² skoro f²(x) = a², to f(x) = a (jeżeli a >0) lub f(x) = − a (jeżeli a <0). Rysujemy wykres h(x) = (x−3)(x−1), nasza f pokrywa się z h tam, gdzie h(x) ≥ 0, zaś jest równa −h tam, gdzie h(x) <0..

Omikron: Agata, w przedziale (−∞,−1) x+1 jest dodatnie czy ujemne?

Agata: ujemnie?

Agata: takie niby proste ,nie czaje jak to przekształcać ?

Krzysiek: Czyżby ? .

Omikron: Skoro jest ujemne w tym przedziale to |x+1|=? (opuść moduł)

Agata: −x+1

Agata: .

Agata: lol

Omikron: Nie

Omikron: Musisz zmienić znak, czy opuszczając moduł stawiasz przed nim − −(x+1)=−x−1

Omikron: *czyli

Agata: ale to do którego jest przykładu? bo sie pogubilam

Agata: −x−1 juz rozumiem,a który to przyklad?

Omikron: W przykładzie c to masz, ale ogólnie taką zasadę się stosuje. Rysuj sobie wykres wyrażenia wewnątrz modułu i sprawdzaj kiedy jest ujemne, a kiedy nieujemne. Dziel na odpowiednie przedziały i zdejmuj moduł.

Krzysiek: I tak zaraz dostaniesz odpowiedz Nie czaję tego

Agata: Dzieki Omikron już rozumiem