okrąg
goska: bardzo proszę o pomoc

Mam okrąg o środku S=(1,1) i promieniu r=1. W zadaniu miałam napisać równanie prostych
stycznych do okręgu,
| | 3 | | 9 | |
które przechodzą przez punkt P= (−1,−3). Obliczyłam jedną y= |
| x + |
| . I tu |
| | 4 | | 4 | |
pytanie, jak obliczyc drugą?
W obliczaniu pierwszej korzystałam z y−y
0= m(x − x
o)
7 lis 21:09
zef:
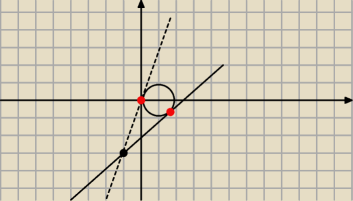
7 lis 21:11
goska: jak to możliwe, jak środek okręgu ma współrzędne s= (1,1) ?
7 lis 21:14
zef:
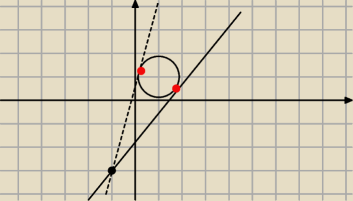
No to taka sytuacja
7 lis 21:16
goska: i jak napisac równanie drugiej prostej?
7 lis 21:20
maniek:
odległość środka okręgu od prostej stycznej jest równa 1.
Daje to równanie z wartością bezwzględną i można obliczyć równania stycznych.
7 lis 21:28
goska: właśnie z tego liczyłam, i wychodzi jedna styczna.
7 lis 21:29
maniek:
styczna: y+3=m(x+1)
y=mx+m−3
postać ogólna: mx−y+m−3=0
odległość środka S(1,1) okręgu od tej prostej:
7 lis 21:32
maniek:
(2m−4)2=m2+1
7 lis 21:33
goska: przepraszam, źle w zadaniu napisałam, r=2
7 lis 21:36
maniek:
wtedy druga styczna ma równanie : x=−1 ...z rysunku....
albo na wyjściu wziąć równanie ogólne prostej :Ax+By+C=0
−A−3B+C=0−−−−−>
C=A+3B
Ax+By+A+3B=0 i teraz odległość
7 lis 21:40
 Mam okrąg o środku S=(1,1) i promieniu r=1. W zadaniu miałam napisać równanie prostych
stycznych do okręgu,
Mam okrąg o środku S=(1,1) i promieniu r=1. W zadaniu miałam napisać równanie prostych
stycznych do okręgu,

 No to taka sytuacja
No to taka sytuacja