 1 sposób
Okrąg opisany na trapezie jest też opisany na ΔABC
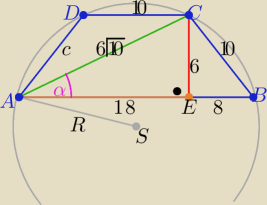
|BC|= 10 , |EB|=8 , |AE|= 18
1 sposób
Okrąg opisany na trapezie jest też opisany na ΔABC
|BC|= 10 , |EB|=8 , |AE|= 18
| 1 | ||
z tw. Pitagorasa w ΔAEC: |AC|=√182+62 ⇒ |AC|= 6√10 to sinα= | ||
| √10 |
| 10 | ||
2R= | ⇒ R= 5√10 | |
| sinα |
| a*c*d | ||
w ΔABC R= | , P(ABC)= 13*6 | |
| 4 P(ABC) |
| 26*10*6√10 | ||
to R= | ⇒ R= 5√10 | |
| 4*13*6 |