wypukłość i wklęsłość Andzia:

	1
Określ przedziały wypukłości i wklęsłości funkcji y=
	lnx

zef:

	1		−1x		−1		2lnx
[		]'=		=		[lnx*lnx]'=
	lnx		ln2x		xln2x		x

	1		2lnx   −(ln2x+x* )   x		ln2x+2lnx		ln+2
−[		]'=−		=		=
	xln2x		x2ln4x		x2ln4x		x2ln3x

Masz drugą pochodną.

Andzia: punkt przegięcia to e⁻² tak?

zef: Tak

Andzia: czyli wklęsła (0;e⁻²) wypukła (e⁻²;1) i (1;+∞) ? Ale cos mi sie wydaje że źle xd

Janek191:

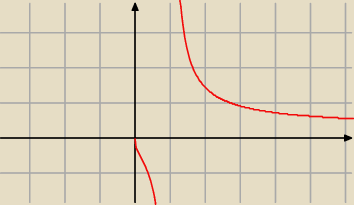
Janek191: f jest wypukła ( 0, e⁻² ) ( 1 ; +∞) f jest wklęsła ( e⁻²; 1)

Andzia: Na jakiej stronie rysujesz te wykresy?

Janek191: Niżej jest napis rysuję Kliknij na rysuję

Andzia: A... dziękuję

Andzia: Zbiór wartości tej funkcji to (−∞;0) (0;+∞)?

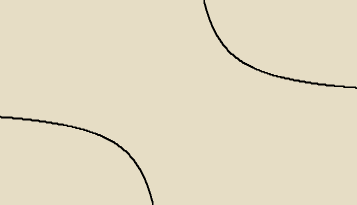
Andzia: nie umiem korzystać z tego rysowania xd

Janek191: To nie takie proste, jak się nie wie Kliknij na znaczek układu współrzędnych i przenieś go na pokratkowany prostokąt Do prostokąta y = wpisujemy wzór funkcji i klikamy na rysunek obok z wykresem funkcji

Andzia: O kurczaki to sobie daruje to rysowanie na razie xd

Andzia:

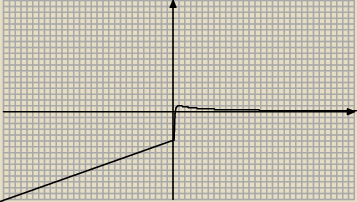
	1+lnx
Wyszło mi coś takiego do y=
	x

Źle prawda? xd

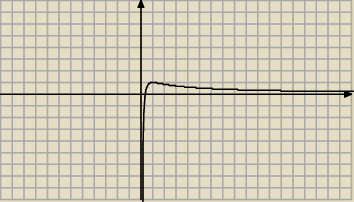
zef: Dobrze tylko czasem przy rysowaniu wkrada się ta kreska, w tym przypadku po lewej (ta od (−∞;0))

Andzia: Ekstremum tej funkcji jest dla x=1 i jest to ekstremum maksimum czy minimum? Bo w odpowiedziach mam minimum a według mnie to maksimum xd

zef: Jak wyszła ci pochodna ?

Andzia: I ta funkcja jest wklęsła dla (0;e^0,5) a wypukła dla (e^0,5;+∞) Zgadza się?

Andzia:

	−lnx
pierwsza pochodna
	x2

zef: Tak jest dobrze, a druga ?

Andzia:

	2lnx−1
druga
	x3

Andzia: czyli ekstremum maksimum tak?

zef: Druga pochodna źle bo:

2xln+x
	=0 tych iksów skrócić nie można bo, xlnx=lnxx
x4

zef: Tak, ekstremum maksimum

Andzia: To nie można wyłączyc x przed nawias?

Andzia: Ale punkt przegięcia mi się zgadza z odpowiedzią xd

zef: Chwila, tam można wyłączyć bo jeszcze dalej w liczniku jest x więc też się skróci, dobrze jest

Andzia: uff.. to dobrze bo bym robiła od nowa xd

zef:

2lnx+1
	=0 x≠0
x3

2lnx=−1

	−1
lnx=
	2

x=e^−0,5 to jest punkt przegięcia

Andzia: A nie e^0,5

zef: Tak, tak źle przepisałem drugą pochodną, błąd w znakach zamiast w liczniku 2lnx−1 dałem 2lnx+1.

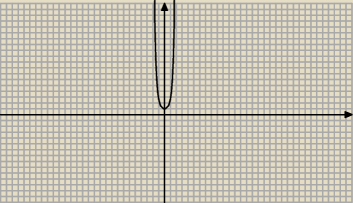
Andzia: A ten wykres jest dobrze? Dla y=e^(−x)2

zef: (0;e^0,5) → wklęsła (e^0,5;∞) → wypukła Co do funkcji e^(−x)2 to się zgadza wykres

Andzia: Ta funkcja jest parzysta tak?

zef: e^(−x)2 tak, widać z wykresu

Andzia: a jak obliczyć asymptotę ukośną?

	e(−x)2
doszłam do		i nie wiem co dalej
	x

zef: Z asymptotą ukośną nie pomogę :< Wiem jedynie że trzeba coś kombinować z granicami, a że jestem jeszcze w liceum to asymptot ukośnych nie miałem, z resztą tego co przed chwilą pisałem też nie Zaraz ktoś powinien pomóc.

Andzia: ok i tak dużo mi już pomogłeś xd dziękuje