AB| = 5:6 a kąt CAB = 60stopni
zad4. W trójkącie ABC wyskość CD dzieli bok AB na odcinki. Na jakie części zostanie podielony
bok lBCl = 18 symetralną boku AB
zad.5 W trapezie równoramiennym ABCD krótsza podstawa ma długość 4 cm a ramie AD 10 cm.
Wysokość DE trapezu przecina przekątna AC w punkcie M tak , ze lMCl:lAMl=2:3. Oblicz długość
drugiej podstawy i długość przekątnej.
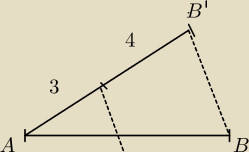zad. 1
narysuj odcinek AB
dorysuj inny odcinek i odmierz na nim 3 cm i 4 cm
połącz koniec odcinka 4centymetrowego z B
narysuj róenoległą do B'B tak jak wyżej
i podzielone
!
sprawdź te zadanie 3 czy coś wiadomo jest o Δ, może jest prostokątny
zobacz co wychodzi wedłóg treści twego zadania
bok CB jest w ruchomy, nie ma danych co do niego
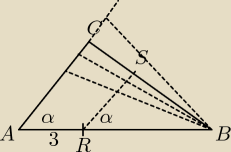
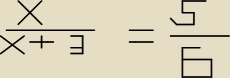Na boku ab trojkąta ABC przez punkt R odległy o 3 cm od wierzchołka A poprowadzono prostą
równoległa do boku AC przecinająca bok BC w punkcie S . Oblicz boki trojkąta ABC,wiedzac ze l
rs l = 15 cm lrbl : lavl = 5:6 a kat CAB = 60 stopni
A oto odpowiedz od innego uzytkownika
Odkładasz odcinek CR i masz trójkąt prostokątny, gdzie kąt CAB ma 60 stopni, dodatkowo masz
AR=3, więc z własności trójkąt możesz policzyć bok CA.
co teraz napsialem i inny uzytkownik podal takie rozwiazanie i nie wiem jak
dalej 
a BC to ile
?
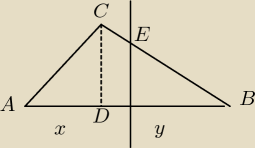zad.4
AD=x
DB=y
CB=18
CE=? AB=x+y
EB=?
| CB | BE | ||
= | |||
| DB | 12AB |
| 9(x+y) | ||
BE= | ||
| y |
| 9(y−x) | ||
CE=18−BE= | ||
| y |
| BE | x+y | ||
= | |||
| CE | y−x |
pomoże ... to pewnie Ci pomogą
| RB | |
=56 | |
| do czego |
| RS | 6RS | 6*15 | |||
=56 → AC+ | = | =18
| |||
| AC | 5 | 5 |
| RS | 5 | x | |||
= | = | →x=15
| |||
| AC | 6 | 3+x |
