tales
super pilne prosze was : zad1. podziel dany odcinek w stosunku 3:4
zad.2 Podstawy trapezu są równe 18 cm i 12 cm. O ile centymetrow nalezy przedłużyc ramię
trapezu długości 6 cm aby przecieło sie z przdłużeniem drugiego ramienia ?
zad3. Na boku AB trojkata ABC przez punkt R odległy o 3 cm od wierzchołka A poprowadzono prostą
równoległą do boku AC przecinającą bok BC w punkcie S.Oblicz boki trójkąta ABC,wiedząc , ze
|RB|: |AB| = 5:6 a kąt CAB = 60stopni
zad4. W trójkącie ABC wyskość CD dzieli bok AB na odcinki. Na jakie części zostanie podielony
bok lBCl = 18 symetralną boku AB
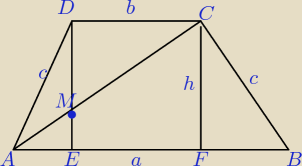
zad.5 W trapezie równoramiennym ABCD krótsza podstawa ma długość 4 cm a ramie AD 10 cm.
Wysokość DE trapezu przecina przekątna AC w punkcie M tak , ze lMCl:lAMl=2:3. Oblicz długość
drugiej podstawy i długość przekątnej.
10 sty 19:10
Anna: Ale tego masz

! Może choć część Ci zrobię.
1) Tu wykonaj konstrukcję dowolnego docinka na 7 równych części (chyba ją znasz

)
i zaznacz punkt dzielący w odległości 3 części od jednego z końców odcinka.
Zaraz poślę kolejne.
10 sty 19:19
super pilne prosze was :
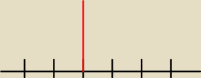
tak ma wygladac 1 zadanie

10 sty 19:27
super pilne prosze was : prosze odpisz z rozwiazaniem

10 sty 19:30
Anna:
18x = 12(x + 6)
18x = 12x + 72
6x = 72 ⇒
x = 12 cm
3) Sprawdź, czy nie opuściłeś jakiegoś słowaw tym zadaniu, bo coś tu brakuje.
c.d.n.
10 sty 19:59
Anna: Zad. 1 : Wynik konstrukcji dobry, pod warunkiem, że wykonałeś to konstrukcyjnie.
10 sty 20:01
kto pomorze????: Na boku ab trojkąta ABC przez punkt R odległy o 3 cm od wierzchołka A poprowadzono prostą
równoległa do boku AC przecinająca bok BC w punkcie S . Oblicz boki trojkąta ABC,wiedzac ze l
rs l = 15 cm l rb l : l abl = 5:6 a kat CAB = 60 stopni
A oto odpowiedz od innego uzytkownika Odkładasz odcinek CR i masz trójkąt prostokątny, gdzie
kąt CAB ma 60 stopni, dodatkowo masz AR=3, więc z własności trójkąt możesz policzyć bok CA.
10 sty 20:02
kto pomorze????: wiec wychodzi mi ze AB = 18 ac = 6 bc =

10 sty 20:03
kto pomorze????:
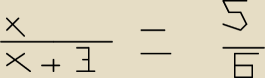
x to dlugosc odcinka rb
10 sty 20:05
Anna:
Dziękuję za poprawienie treści. Zaraz napiszę rozwiązanie. Ale
kto pomoże

,nie można
obliczyć AC tak, jak proponujesz, gdyż nie wiemy, że wysokością jest CR.

10 sty 20:12
kto pomorze????: to prosze o odpiwedz do 4 i5 odcinka dziekuje ci za pomoc

10 sty 20:13
Anna:
6(AB − 3) = 5 AB
6 AB − 18 = 5 AB
IABI = 18
IRSI = IRBI i α = 60
0 ⇒ ΔRSB jest równoboczny
Zatem IACI = IBCI = IABI = 18 cm
10 sty 20:23
kto pomorze????: a na 4 i 5 bym porosil

10 sty 20:32
Anna:
| | MC | | 2 | |
5) b = CD = 4 cm, c = 10 cm, |
| = |
| a, AC = ? |
| | AM | | 3 | |
ΔAEM ∼ Δ CDM ( cecha kk)
FB = AE = 6
a = b + AE + FB = 4 + 6 + 6 =
16
Z ΔCFB obliczam h:
h
2 + FB
2 = c
2
h
2 = 100 − 36 = 64 ⇒
h = 8
Z ΔAFC obliczam AC:
AC
2 = AF
2 + h
2
AC
2 = 100 + 64 = 164 ⇒
AC =
√164 =
2√41
10 sty 20:46
kto pomorze????: oj dziekuje wielka jestes

10 sty 20:54
adam: 1, Podziel odcinek A,B w stosunku 3:5
18 mar 21:57
anna: Podziel dany odcinek na 8 równych części, za pomocą symetralnych i zaznacz punkt dzielący,
odległy o 3 jednostki od jednego z końców odcinka AB.
18 mar 22:49
 ! Może choć część Ci zrobię.
1) Tu wykonaj konstrukcję dowolnego docinka na 7 równych części (chyba ją znasz
! Może choć część Ci zrobię.
1) Tu wykonaj konstrukcję dowolnego docinka na 7 równych części (chyba ją znasz  )
i zaznacz punkt dzielący w odległości 3 części od jednego z końców odcinka.
Zaraz poślę kolejne.
)
i zaznacz punkt dzielący w odległości 3 części od jednego z końców odcinka.
Zaraz poślę kolejne.
 tak ma wygladac 1 zadanie
tak ma wygladac 1 zadanie 


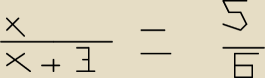 x to dlugosc odcinka rb
x to dlugosc odcinka rb

 ,nie można
obliczyć AC tak, jak proponujesz, gdyż nie wiemy, że wysokością jest CR.
,nie można
obliczyć AC tak, jak proponujesz, gdyż nie wiemy, że wysokością jest CR. 



