Cieakwe zadanko
Saizou :
Cześć wam, przeglądając zadania, natrafiłem się na dość ciekawe zadanie
Znaleźć odległość między dwoma nieprzecinającymi się przekątnymi dwóch sąsiednich ścian
sześcianu o krawędzi długości 1.
6 lis 17:34
g:
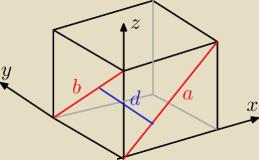
Przekątne przedstawiam parametrycznie:
a: x=p; y=0; z=p
b: x=0; y=1−q; z=q
Odległość między prostą 'a' i punktem B leżącym na 'b':
|aB| = ∥ (A−B) x [1/
√2; 0; 1/
√2] ∥ =
= ∥ [0; 1−q; q] x [1; 0; 1] ∥ /
√2 = ∥ [1−q; q; 1−q] ∥ /
√2
|aB|
2 = [3q
2 − 4q + 2] / 2
minimum |aB|
2 osiaga dla q=2/3 i to minimum = 1/3
d = 1/
√3
6 lis 18:30
Eta:
Rację ma
g 
Kasuję to co podałam

6 lis 18:41
jc: d = 1/
√3 
6 lis 18:44
6 lis 18:45
Mila:
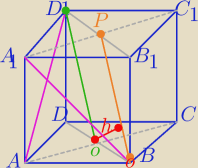
Sposób dla LO.
1)
OD1 − Rzut AD
1 na płaszczyznę DBB
1D
1
2)
PB − rzut A
1B na na płaszczyznę DBB
1D
1
3) odległość między rzutami to odległość prostych skośnych OD
1 i PB
P
OBPD1=|BP|*h
| | a√2 | | 3 | |
|BP|2=a2+( |
| )2= |
| a2 |
| | 2 | | 2 | |
========
6 lis 21:42
Eta:

6 lis 21:44
Saizou :
Dziękuję bardzo, właśnie poszukiwałem odpowiedzi na poziomie LO.
Dziękuję Wszystkim
6 lis 21:52
Mila:

6 lis 21:53
Kacper:

6 lis 21:54
Metis:

6 lis 21:56
Eta:
I
Mila pięknym rozwiązaniem
wywołała Wszystkich .......

6 lis 22:07
Saizou :
Owszem, ja ostatnio nie mam czasu aby udzielać się na forum :c
6 lis 22:11
Eta:
Często jesteś na forum

Pewnie śledzisz rozwiązania zadań z ..........
planimetrii
bo to najpiękniejszy dział matematyki

6 lis 22:17
Saizou :
To że jestem nie oznacza że się udzielam xd
Planimetria jest spoko, nawet mam taki przedmiot na studiach xd
6 lis 22:20
Mila:
Bardzo mnie cieszy takie miłe i wspaniałe towarzystwo.

6 lis 22:20
6 lis 22:21
Saizou :
Milu będę mieć do Ciebie sprawę, ale to się odezwę we wtorek

6 lis 22:30
Metis: Benny gdzie się podziewasz

?
6 lis 22:34
Benny: Wszędzie mnie pełno

6 lis 22:38
b.: Cieszę się, że pojawiło się rozwiązanie bez użycia geometrii analitycznej, też się nad tym
zastanawiałem, ale przyznam, że tego rozwiązania nie rozumiem.
Dlaczego rzutujemy akurat na płaszczyznę DBB1D1? Tj. dlaczego wtedy odległość między rzutami
to odległość między prostymi?
Bo oczywiście nie każda płaszczyzna będzie miała taką własność, trzeba ją wybrać specjalnie.
6 lis 22:38
Ajtek:
To ja się tylko przywitam, bry wieczór obecnym

6 lis 22:39
Metis: bry, bry

6 lis 22:40
Mila:
Zauważ b, że prosta AD1 i prosta A1B leżą teraz w płaszczyznach równoległych:
AOD1 i A1BP przy czym D1O ||SB.
Tak to rozumiem.
Może lepiej wyjaśni ktoś, kto miał "kreski" na studiach.
6 lis 23:39
b.: No tak, i te płaszczyzny równoległe są prostopadłe do płaszczyzny DBB1D1, na którą rzutujemy.
Już rozumiem, dzięki.
7 lis 08:32
Mila: 
7 lis 16:16
s:

27 kwi 20:24
ehh: Pozdrawiam wszystkich, super rozwiązanie

27 kwi 20:27
 Przekątne przedstawiam parametrycznie:
a: x=p; y=0; z=p
b: x=0; y=1−q; z=q
Odległość między prostą 'a' i punktem B leżącym na 'b':
|aB| = ∥ (A−B) x [1/√2; 0; 1/√2] ∥ =
= ∥ [0; 1−q; q] x [1; 0; 1] ∥ / √2 = ∥ [1−q; q; 1−q] ∥ / √2
|aB|2 = [3q2 − 4q + 2] / 2
minimum |aB|2 osiaga dla q=2/3 i to minimum = 1/3
d = 1/√3
Przekątne przedstawiam parametrycznie:
a: x=p; y=0; z=p
b: x=0; y=1−q; z=q
Odległość między prostą 'a' i punktem B leżącym na 'b':
|aB| = ∥ (A−B) x [1/√2; 0; 1/√2] ∥ =
= ∥ [0; 1−q; q] x [1; 0; 1] ∥ / √2 = ∥ [1−q; q; 1−q] ∥ / √2
|aB|2 = [3q2 − 4q + 2] / 2
minimum |aB|2 osiaga dla q=2/3 i to minimum = 1/3
d = 1/√3



 Sposób dla LO.
1) OD1 − Rzut AD1 na płaszczyznę DBB1D1
2) PB − rzut A1B na na płaszczyznę DBB1D1
3) odległość między rzutami to odległość prostych skośnych OD1 i PB
Sposób dla LO.
1) OD1 − Rzut AD1 na płaszczyznę DBB1D1
2) PB − rzut A1B na na płaszczyznę DBB1D1
3) odległość między rzutami to odległość prostych skośnych OD1 i PB





 Pewnie śledzisz rozwiązania zadań z .......... planimetrii
bo to najpiękniejszy dział matematyki
Pewnie śledzisz rozwiązania zadań z .......... planimetrii
bo to najpiękniejszy dział matematyki 








 ?
?






