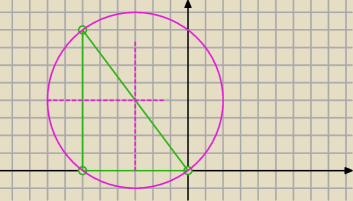
okrąg Ania: napisz równanie okręgu przechodzącego przez punkty A, B, C, jeśli: A(0,0), B(−6,0), C(−6,8) skorzystaj z okręgu opisanego na trójkącie o środku będącym przecięciem symetralnych, weź pod uwagę dwa jego boki proszę o pomoc

===:

jcb: można prościej (x−a)²+(y−b)²=r² Podstaw punkty i rozwiąż układ równań

===: Punkty są specyficzne Wprost zna współrzędne środka okręgu a promień jako √16+9 ... czyli równanie ma gotowe i niczego z układu trzech równań szukać nie musi

PW: Nie, === podał najprostszy sposób: zauważyć, że ABC tworzą trójkąt prostokątny, a więc środek okręgu opisanego leży w połowie przeciwprostokątnej (a promień to połowa długości przeciprostokątnej).