


 Dobry rys, załatwia wszystko w tym zad,
tylko ,że mistrzem w rysowaniu jest Bogdan
Dobry rys, załatwia wszystko w tym zad,
tylko ,że mistrzem w rysowaniu jest Bogdan  Postaram się jakoś Ci to zad. objaśnić.
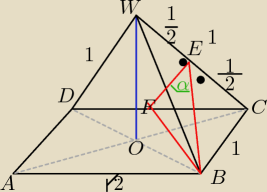
trójkąt w ścianie BCW jest równoboczny o boku dł 1
trójkąt w ścianieCDW jest prostokątny i równoramienny o ramionach dł. 1
i podstawie ICDI= √2 ( z treści zadania)
cosα −−− wyznaczymy z tw. cosinusów w czerwonym trójkącie
zatem : potrzebne będą długości : IBEI , IFEI i IBFI
Postaram się jakoś Ci to zad. objaśnić.
trójkąt w ścianie BCW jest równoboczny o boku dł 1
trójkąt w ścianieCDW jest prostokątny i równoramienny o ramionach dł. 1
i podstawie ICDI= √2 ( z treści zadania)
cosα −−− wyznaczymy z tw. cosinusów w czerwonym trójkącie
zatem : potrzebne będą długości : IBEI , IFEI i IBFI
| 1*√3 | √3 | |||
IBEI= hΔBCW = | = | |||
| 2 | 2 |
| √2 | ||
to IFEI= 12 i IFCI = | ||
| 2 |
| (12)2 +( √32)2 − 32 | ||
cosα= | =........dokończ
| |
| 2*12*√32 |
| √3 | ||
otrzymasz: cosα= − | ||
| 3 |
| √6 | ||
więc sinα= √1− (1/3)= √2/3= | ||
| 3 |
| √2 | ||
ctgα= − | ||
| 2 |
 Twój rysunek jest wystarczający
Twój rysunek jest wystarczający  Dzięki i pozdrawiam!
Dzięki i pozdrawiam! 
