Liczby zespolone w=z/(iz+4) Haze323: Narysuj zbiór wszystkich liczb zespolonych dla których a) w jest liczbą rzeczywistą b) w jest liczbą urojoną w=^Z _iZ+4 Bardzo proszę o pomoc oraz o wytłumaczenie krok po kroku rozwiązania

Mila: A jak próbowałeś?

Haze323: Szczerze to nawet nie wiem jak zacząć. Próbowałem pomnożyć górę i dół przez liczbę sprzężoną do mianownika, ale to chyba nie tędy droga.

Mila: Dobrze zacząłeś, teraz jestem chwilowo zajęta, po 17 pomogę. z=x+iy gdzie x,y∊R

	(x+iy)		(x+iy)
w=		=		=
	i*(x+iy)+4		ix−y+4

	(x+iy)		(x+iy)*[(−y+4)−x]
		=		=
	(−y+4)+ix		(−y+4)2+x2

Wymnóż w liczniku, ja później napiszę resztę

Mila: Zgubiłam i w liczniku:

(x+iy)*[(−y+4)−ix]
y2−8y+16+x2

Haze323: Licznik mi wyszedł (4x−x²)+(4y−y²)i. Czy teraz mam to traktować jako wyrazy liczby zespolonej (a + bi) i podzielić przez mianownik?

Mila:

	−xy+4x−x2*i−y2i+4y i−xyi2
w=		=
	(y−4)2+x2

	4x−xy+xy+i*(−x2−y2+4y)
=		=
	(y−4)2+x2

	4x+i*(−x2−y2+4y)
=		=
	(y−4)2+x2

	4x		(−x2−y2+4yi)
=		+		*i
	(y−4)2+x2		(y−4)2+x2

w∊R⇔

(−x2−y2+4y)
	=0 i x≠0 i y≠4
(y−4)2+x2

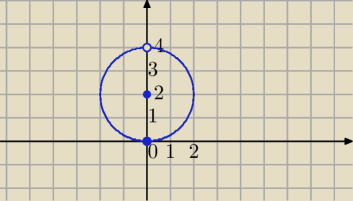
−x²−y²+4y=0 /*(−1) x²+y²−4y=0 x²+(y−2)²=4 okrąg S=(0,2) r=2 z≠(0,4) Sprawdź (0,0)

Haze323: Dzięki wielkie . Mam jeszcze jedno pytanie, czy ten zbiór tyczy się liczb rzeczywistych i urojonych czy tylko rzeczywistych?

Mila: Napisałam w∊R teraz: w− czysto urojona⇔

4x
	=0⇔
(y−4)2+x2

4x=0 i y−4≠0⇔ x=0 i y≠4⇒ będzie oś y bez punktu (0,4) i (0,0) punkty (0,y) i y≠4 1) dla punktu (0,4) czyli dla z=4i mamy

	4i		4i
w=		=		sprzeczność
	i*4i2+4		0

2) dla z=0 mamy

0		0
	=		=0 liczba rzeczywista
i*0+4		4

3) z=0+iy i y≠4 i y≠0

	iy		yi
w=		=		liczba czysto urojona.
	i*iy+4		−y+4