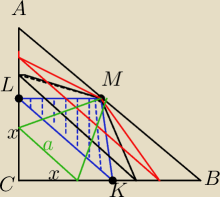
 W trojkacie ABC jest AB=2 i AC=BC .
∡ACB=90o
W trojkat ABC wpisano trojkat LMK tak ze M jest srodkiem AB . Punkt L ∊AC ,a punkt K∊BC i
KL||AB
Zbadaj pole trojkata LMK jako funkcje dlugosci odcinka CL . Sporzadz wykres
x= dlugosc CL
y=SLMK
Bedzie to trojkat postokatny rownoramienny
Skoro AB=2 to AC=BC=√2
Narysowalem sobie pare trojkatow LMK i widze ze beda to trojkaty rownoranienne
gdzie podstawa (a) tego trojkata wynosi a= √2x
Teraz do wyliczenia pola tego trojkata potrzebuje wysokosc
Wysokosc oblicze z twierdzenia Pitagorasa ale musze miec dlugosc odcinka LM policzona
Ale proszse o podpowiedz jak policzyc
W trojkacie ABC jest AB=2 i AC=BC .
∡ACB=90o
W trojkat ABC wpisano trojkat LMK tak ze M jest srodkiem AB . Punkt L ∊AC ,a punkt K∊BC i
KL||AB
Zbadaj pole trojkata LMK jako funkcje dlugosci odcinka CL . Sporzadz wykres
x= dlugosc CL
y=SLMK
Bedzie to trojkat postokatny rownoramienny
Skoro AB=2 to AC=BC=√2
Narysowalem sobie pare trojkatow LMK i widze ze beda to trojkaty rownoranienne
gdzie podstawa (a) tego trojkata wynosi a= √2x
Teraz do wyliczenia pola tego trojkata potrzebuje wysokosc
Wysokosc oblicze z twierdzenia Pitagorasa ale musze miec dlugosc odcinka LM policzona
Ale proszse o podpowiedz jak policzyc
| x√2 | ||
h= 1− | ||
| 2 |
 Teraz pole tego trojkata moge zapisac tak
Teraz pole tego trojkata moge zapisac tak
| x√2 | x√2 | |||
y= | (1− | ) | ||
| 2 | 2 |

| x√2 | 2x2 | |||
y= | − | i 0<x<√2 | ||
| 2 | 4 |
| x√2 | x2 | |||
y= | − | |||
| 2 | 2 |
| √2 | √2 | |||
xmax = − | {−1}= | = 0,5AC | ||
| 2 | 2 |
| 1 | 2 | 1 | ||||
ymax}= | − | = | ||||
| 2 | 8 | 4 |
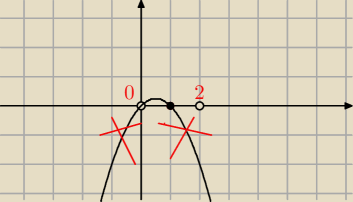
 Miejsca zerowe P(x) to
x=0,x=√2
Miejsca zerowe P(x) to
x=0,x=√2
| 1 | √2 | |||
P(x)=− | x2+ | x | ||
| 2 | 2 |
| √2 | ||
xw= | ||
| 2 |
| 1 | ||
ymax= | ||
| 4 |
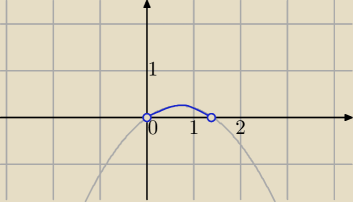
 Teraz juz wiem ze tylko ta czesc mad osia OX .
Zle wpisalem do programu rysujacego wykresy (teraz to zauwazylem .
Teraz juz wiem ze tylko ta czesc mad osia OX .
Zle wpisalem do programu rysujacego wykresy (teraz to zauwazylem .