geometria analityczna Kamil: Bardzo proszę o pomoc, krok po kroku co trzeba tu zrobić Nie mogę korzystać z okręgu. W trójkącie prostokątnym ABC (|<ABC|=90stopni) dwa wierzchołki mają współrzędne A(4,−5) i C(−8,5). Wyznacz współrzędne wierzchołka B, wiedząc, że pole ΔABC jest równe 61.

5-latek : Wyjasnij mi co to znaczy Nie moge korzystac z okregu ?

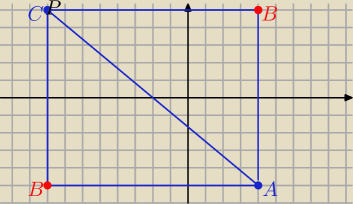
Eta: P(ABC)=60 ( a Ty napisałeś 61 odp: B( −8,−5) lub B( 4, 5)

Kamil: B(3,6) lub B(−7,−6) Napisałem jak jest w książce Eto.

Kamil: @5−latek widziałem rozwiązania tego zadania z wykorzystaniem wpisywania okręgu w trójkąt, mam to zrobić bez układu współrzędnych i dorysowywania okręgu

===: 1. Napisz równanie prostej przez A i C i przekształć do postaci ogólnej 2. Znając pole trójkąta wyznacz jego wysokość opuszczoną na bok AC Będzie to odległość punktu B od prostej 3. Układaj równanie na odległość punktu od prostej itd

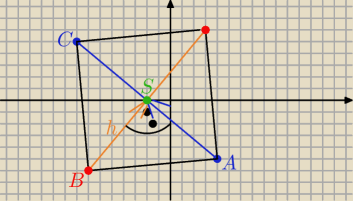
Eta: Sorry za wcześniejsze ( myślałam,że pole ma być 60 2 sposób jeżeli P= 61 to można też za pomocą wektorów B(x,y)

	2P
|AC|=2√61 to |AS|=√61 i z pola h=		⇒ h=√61
	|AC|

zatem |BS|= |AS|=√61 i wektory AS i BS są prostopadłe i równej długości S( −2,0) AS=[6,−5] to z warunku prostopadłości BS= [5,6] lub [ −5, −6] BS=[ −2−x, −y] ⇒ −2−x=5 i −y=6 lub −2−x= −5 i −y= −6 x= −7 i y=−6 lub x= 3 i y= 6 B(3,6) lub B( −7 , −6)

Kamil: dziękuję

Eta:

piotr: a,b przyprostokątne a*b=122; a²+b²=244 ⇒ a=√122 i b=√122 (x−4)²+(y+5)²=122; (x+8)²+(y−5)²=122 ⇒ x=−7, y=−6 lub x=3, y=6