rozwiąz nierówność
OLa: Prosze o pomoc w rozwiązaniu, mam juz wynik ale nwm czy dobrze rozwiązałam.
Jesli chodzi o dziedzine to można to zapisać tak R\{−1,1} czy lepiej przedziałem
x∊(−
∞,−1)∪(1,
∞) ?
3 lis 20:03
zef: R\{−1,1} ≠ x∊(−∞;−1)u(1;∞)
3 lis 20:12
jcb:
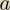
1 zapis jest poprawny
| x2−5x+3 | | x2−5x+3 | |
| ≤1 lub |
| ≥−1 |
| x2−1 | | x2−1 | |
| x2−5x+3 | | x2−5x+3 | |
| −1≤0 lub |
| +1 ≥0 |
| x2−1 | | x2−1 | |
| x2−5x+3−x2+1 | | x2−5x+3+x2−1 | |
| ≤0 lub |
| ≥0 |
| x2−1 | | x2−1 | |
| −5x+4 | | 2x2−5x+2 | |
| ≤0 lub |
| ≥0 |
| x2−1 | | x2−1 | |
(−5x+4)(x
2−1)≤0 lub 2x
2−5x+2)(x
2−1)≥0
x=4/5 x=1 x=−1 x=1 x=−1 Δ=9 ⇒
√Δ=3
x=1/2 x=2
rysujemy osie liczbowe
x∊(−1,4/5>∪(1,+
∞) lub x∊(−
∞,−1)∪<1/2,1)∪<2,+
∞)
na wspolna os oba rozw i mamy:
x∊<1/2,4/5>∪<2,+
∞)
3 lis 20:25
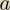 1 zapis jest poprawny
1 zapis jest poprawny