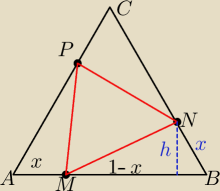
kwadratowa.... 5-latek : Dany jest trojkat rownoboczny ABC Na bokach AB ,BC i CA zaznacz odpowiednio punkty M N P tak ze AM=BN+CP=x i AB=1 dm Zbadaj pole trojkata MNP jako funkcje x y=P_MNP= P_ABC−3P_MBN

	√3
PABC=
	4

Teraz licze pole trojkata MNB

	1		x*√3
PMNB=		*(1−x)*
	2		2

h wyznaczylem z trojakta 30,60,90.

	x√3		x2√3
PMNB=		−
	4		4

	√3		x√3		x2√3
y=		−3*(		−		)
	4		4		4

po uporzdkowaniu

	√3
y=		(1−3x+3x2)
	4

	3
xnim =		= 0,5
	6

	√3		√3
ymin=		(1−1,5+0,75)=
	4		16

Prosze sprawdzic

Eta: ok 2 sposób Z tw. kosinusów możesz wykazać ,że trójkąt MNP jest równoboczny b²= 3x²−3x+1

	√3
P(MNP)(x)=		(3x2−3x+1)
	4

	√3
xw= 0,5 to yw = Pmin=P(0,5)= ..... =
	3

Eta: i założenie : x∊(0,1)

5-latek : Dzien dobry Eta dziekuje za sprawdzenie i pokazanie 2 sposobu .

Eta: Na zdrowie

jc: AM=BN+CP. Skąd wiesz, gdzie leżą punkty N, P?

Eta: Źle wcisnął klawisz "=" "+" AM=BN=CP=x

5-latek : Tak jc zle wcisnalem mialobyc [=] Soprawdzalem dwa razy i wydawalo mi sie ze bylo dobrze (a jednak nie .