Przedstaw graficznie, liczby zespolone
Mati: Przedstaw graficznie:
|iz−1|≥|Z+1+i|
|i|*|z+i|≥|z+1+i|
|z−(−i)|≥|z−(−1−i)|
Jak to przedstawić ?
2 lis 15:42
Mati: Ktoś potrafi to pokazać?
2 lis 17:32
PW: Jeżeli pokazałeś kolejne przekształcenia, to trzecia linijka źle, po lewej stronie
|−z+i2| = |−z − 1| = |z+1|
2 lis 17:51
Mila:
|iz−1|≥|z+1+i|
|iz+i
2|≥|z−(−1−i)|
|i|*|z+i|≥|z−(−1−i)|⇔
|z−(−i)|≥|z−(−1−i)|
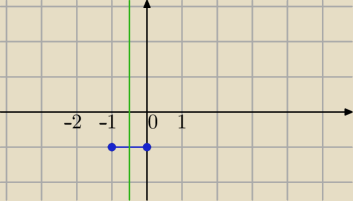
Rysujesz symetralną odcinka o końcach (0,−1) i (−1,−1)
| | 1 | |
półpłaszczyzna na lewo od symetralnej x=− |
| |
| | 2 | |
Albo
algebraicznie

z+i|≥|z+1+i|
z=x+iy, gdzie x, y ∊R
|x+i(y+1)|≥|(x+1)+(y+1)i|
√x2+(y+1)2≥
√(x+1)2+(y+1)2
2 lis 17:52
PW: Nie, dobrze jest.
Teraz rysujesz zbiór punktów, dla których
|z+i| = |z+i+1|.
czyli symetralną odcinka o końcach −i, −(1+i).
2 lis 17:56
Mati: Postać algebraiczna wszystko wyjaśnia. Z wcześniejszej nie wpadłbym na to, że będzie to
symetralna odcinka. Jakaś podpowiedź skąd wiemy, że jest to symetralna?
Wielkie dzięki za pomoc

2 lis 19:26
PW: Symetralna to zbiór punktów jednakowo odległych od końców odcinka. A moduł różnicy to odległość
między liczbami.
Na symetralnej leżą więc punkty, dla których ma miejsce równość. Nierówność ma miejsce dla
punktów leżących po odpowiedniej stronie symetralnej.
2 lis 19:39
Mila:
Postać algebraiczna to wyjaśnia, ale zapamiętaj:
|z−z1|=|z−z2| zbiór punktów leżących na symetralnej odcinka z1z2
2 lis 19:39
Mati: Dzięki

2 lis 20:27
Mila:

2 lis 21:29
 |iz−1|≥|z+1+i|
|iz+i2|≥|z−(−1−i)|
|i|*|z+i|≥|z−(−1−i)|⇔
|z−(−i)|≥|z−(−1−i)|
Rysujesz symetralną odcinka o końcach (0,−1) i (−1,−1)
|iz−1|≥|z+1+i|
|iz+i2|≥|z−(−1−i)|
|i|*|z+i|≥|z−(−1−i)|⇔
|z−(−i)|≥|z−(−1−i)|
Rysujesz symetralną odcinka o końcach (0,−1) i (−1,−1)
 z+i|≥|z+1+i|
z=x+iy, gdzie x, y ∊R
|x+i(y+1)|≥|(x+1)+(y+1)i|
√x2+(y+1)2≥√(x+1)2+(y+1)2
z+i|≥|z+1+i|
z=x+iy, gdzie x, y ∊R
|x+i(y+1)|≥|(x+1)+(y+1)i|
√x2+(y+1)2≥√(x+1)2+(y+1)2


