 z2+2z*=0
z=x+iy, x,y∊R
x2+2xyi−y2+2(x−iy)=0
x2+2xy i−y2+2x−2y i=0
(x2+2x−y2)+i*(2xy−2y)=0
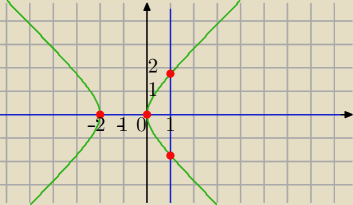
(x2+2x−y2)=0 i (2xy−2y)=0 graficznie , widać 4 rozwiązania
z (2) 2y*(x−1)=0⇔
y=0 lub x=1
1) y=0 to x2+2x=0⇔x(x+2)=0 ⇔x=0 lub x=−2
Mamy dwie liczby
z0=0 lub z1=−2+0i
a) x=0 to (0+2*0−y2)=0 ⇔z=0
b) x=−2 to (−2)2+2*(−2)−y2=0⇔y=0
odp. z=0 lub z=−2
2) x=1
12+2*1−y2=0⇔
y2=3
y=√3 lub y=−√3
z3=1+√3*i lub z4=1−√3*i
odp. z=0 lub z=−2 lub z3=1+√3*i lub z4=1−√3*i
z2+2z*=0
z=x+iy, x,y∊R
x2+2xyi−y2+2(x−iy)=0
x2+2xy i−y2+2x−2y i=0
(x2+2x−y2)+i*(2xy−2y)=0
(x2+2x−y2)=0 i (2xy−2y)=0 graficznie , widać 4 rozwiązania
z (2) 2y*(x−1)=0⇔
y=0 lub x=1
1) y=0 to x2+2x=0⇔x(x+2)=0 ⇔x=0 lub x=−2
Mamy dwie liczby
z0=0 lub z1=−2+0i
a) x=0 to (0+2*0−y2)=0 ⇔z=0
b) x=−2 to (−2)2+2*(−2)−y2=0⇔y=0
odp. z=0 lub z=−2
2) x=1
12+2*1−y2=0⇔
y2=3
y=√3 lub y=−√3
z3=1+√3*i lub z4=1−√3*i
odp. z=0 lub z=−2 lub z3=1+√3*i lub z4=1−√3*i