geometryczna interpretacja nierówności liczb zespolonych patrycja: Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych wyznaczyć i narysować zbiory liczb zespolonych spełniających warunki. I tu wtrącenie: generalnie nie mam problemu gdy po jednej stronie równania jest tylko niewiadoma w wartości bezwzględnej np |z−1|≤4, |z+5i|=|3−4i|. Problem zaczyna mi się, gdy mam po dwóch stronach równania wart. bezwzgl. z niewiadomą, i mam dwa przykłady, jeden już rozwiązałam, ale w notatkach mam zupełnie inny wynik niż mi wyszedł. Nie są to moje notatki dlatego muszę brać pod uwagę, że są niedokładne/ niedokończone. Takie zadanie: a) |z−1|=|1+5i−z|, i liczę: |x+yi−1| = |1+5i −x−yi| |x−1+yi| = |1−x + (5−y)i|, stąd: x−1=1−x, x=1 y=5−y, y=5/2 teoretycznie wychodzi mi jeden punkt do zaznaczenia: (1, 5/2) Ale odpowiedź w notatkach mam, że rozwiązaniem jest dwusieczna odcinka między punktami (1,0) a (1,5) (skąd w ogóle takie punkty się wzięły prowadzącemu), no i rysunek, gdzie jest ta dwusieczna(a właściwie prędzej powinno być jak już symetralna), czyli tak naprawdę po prostu fukncja liniowa y=5/2. Ale skąd prowadzący znalazł takie rozwiązanie? Od razu mówię, że niestety nie mam jak go spytać, bo siedzę chora w domku. Drugi przykład to nierówność z modułem: b) |z+3i|<|z−1−4i| I o ile wyżej, w 1 przykładzie była równość, to jak wiemy w matematyce nierówności nieraz są bardzo kapryśne i nie wiem, czy do końca mogłabym sobie "wyjąć" tak jak w pierwszym przykładzie, odpowiadające sobie zmienne, nie biorąc żadnych dodatkowych założeń pod uwagę. Aha i jeśli ktoś by mógł, prosiłabym o wyjaśnienie, skąd dany algorytm na rozwiązanie takiego zadania. Dziękuję pięknie z góry za pomoc

patrycja: nikt nie pomoże

ICSP: moduł |z − (x − yi)| to odległość punktu z od (x,y) |z − 1| to odległość z od (1 , 0) |1 + 5i − z| = |− [ z − 1 − 5i]| = |−1| * |z − (1 + 5i)| = |z − (1 + 5i)| to odległość z od (1 , 5) Zaznaczasz na płaszczyźnie punkt (1 , 0) oraz (1 , 5) i rysujesz symetralną odcinka o końcach w tych włąśnie punktach. Drugi robisz tak samo. Rozwiązaniem będzie półpłaszczyzna.

ICSP: |z − (x + yi)|, nie wiem dlaczego w pierwszej wersji pojawił się minus

patrycja: Miałam coś napisać jeszcze, ale właśnie jak przeczytałam twoje rozwiązanie dokładnie to wszytsko zrozumiałam. Dzięki

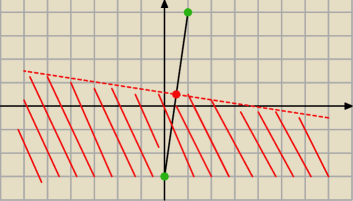
patrycja: Jeszcze tak gwoli ścisłości, żeby sie upewnić, że dobrze rozumiem, w drugim ta półpłaszczyzna to będzie obszar POD prostą prostopadła do odcinka łaczącego punkty (0,−3) i (1,4) (zielone kropki) i przechodząca przez punkt (1/2,1/2) (czerwona kropka) ?

patrycja: ?

patrycja: Mógłby się ktoś jeszcze ustosunkować do mojego przedostatniego posta? (tego z rysunkiem)

ICSP: . To będzie obszar pod prostą. Jeżeli nie jesteś pewna mozesz podstawić dowolny punkt.