W przypadku 3√−8i, |z|=8, cosφ=0, sinφ=−1 ile wynosi φ? yeyo: W przypadku ³√−8i, |z|=8, cosφ=0, sinφ=−1 ile wynosi φ?

yeyo: φ=³₂π?

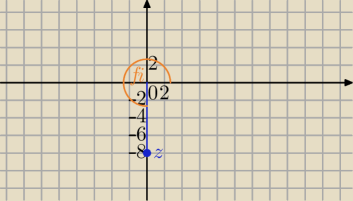
Mila: z=−8i

	3π
φ=
	2

yeyo: @Mila dziękuję serdecznie :~)

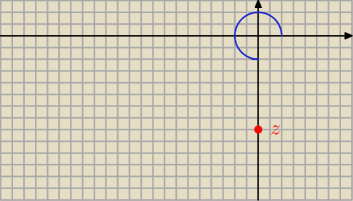
Janek191: φ = 1,5 π

Mila:

Mila: ³√−8i z=−8i |z|=8

	3π
φ=
	2

	3π   +2kπ 2		3π   +2kπ 2
zk=3√8*(cos		+i sin		), k∊{0,1,2}
	3		3

	3π		3π
z0=2*(cos		+i sin		)=2*(0+i)=2i
	6		6

	7π		7π		√3		1
z1=2*(cos		+i sin		)=2*(−		−		i)=−√3−i
	6		6		2		2

	11π		11π		√3		1
z2= 2*(cos		+i sin		)=2*(		−		i)=√3−i
	6		6		2		2

yeyo: @Mila: Takie wyniki również mi wyszły Miałem czarną dziurę z odczytaniem kąta φ, ale już wszystko sobie przypomniałem

Mila: Dobrze.