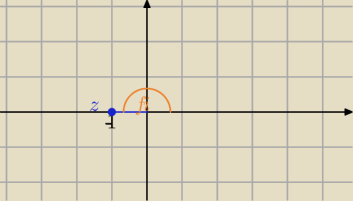
Zespolone yeyo: Gdzie popełniłem błąd? ⁴√−1. Wyszły mi 4 rozwiązania: −> 1;i;−1;−i. |z|=1 cosφ=−1 sinφ=0 2 ćwiartka α₀=π φ=π−π=0

5-latek: NIgdzie nie popelniles bledy (takie maja wyjsc .

ICSP: 1. To nie jest druga ćwiartka 2. Liczba −1 jest rzeczywista i leży na ujemnej półosi osi odciętych, więc φ = π

ICSP: ale spójrz na to z innej strony. Jeżeli ktoś Ciebie poprosi o wyznaczenie pierwiastków : ⁴√1 to masz już gotowe zadanie.

yeyo: ICSP masz rację, możesz mi jeszcze wytłumaczyć czemu φ to jest właśnie π? Zawsze odczytywałem ćwiartki na podstawie znaków, jednak gdy jest 0 to ta metoda nie działa. Miałem jeszcze metodę na płaszczyźnie zespolonej, jednak gdy pojawia się 0 to nie wiem jak odczytać ćwiartkę.

ICSP: ćwiartki odczytujesz tylko gdy cosφ ≠ 0 ∧ sinφ ≠ 0. Jeżeli zeruje się albo sinus albo cosinus to rysujesz płaszczyzne zespoloną, zaznaczasz na niej żadany punkt i odczytujesz kąt.

yeyo: Wszystko jasne, dziękuję Ci serdecznie

||: rozwiązań r−nia ⁿ√−1 jest zawsze n

yeyo: Wiem to, jednak wiedziałem również, że te wypisane przeze mnie są błędne i chciałem doszukać się błędu, ICSP mi jak najbardziej pomógł znaleźć błąd i go zrozumieć

yeyo: A w przypadku ³√−8i, |z|=8, cosφ=0, sinφ=−1 ile wynosi φ?

Mila: φ=π

	π+2kπ		π+2kπ
zk=1*(cos		+i sin		) dla k∊{0,1,2,3}
	4		4

	π		π		√2		√2
z0=cos		+i sin		=		+i
	4		4		2		2

	3π		3π		√2		√2
z1=cos		+i sin		=−		+i
	4		4		2		2

	5π		5π		√2		√2
z2=cos		+i sin		=−		−i
	4		4		2		2

	7π		7π		√2		√2
z3=cos		+i sin		=		−i
	4		4		2		2

yeyo: @Mila dzięki, z tamtym zadaniem się uporałem i wyszły mi takie same wyniki, jednak mam problemy jeszcze z odczytywaniem φ gdy sin lub cos jest równy 0. Co np w przypadku wymienionym przeze mnie wyżej?

yeyo: φ=³₂π?