ciezko misia: tg 3x ≥ 1 3 sin x = 2cos² x

	1
sin2 x≤
	2

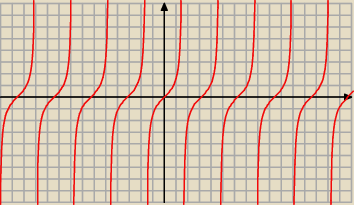
Adamm: tg(3x)≥1=tg(π/4) z rysunku wiemy że równanie spełnia π/4+kπ≤3x<π/2+kπ gdzie k∊ℤ π/12+kπ/3≤x<π/6+kπ/3 x∊<π/12+kπ/3;π/6+kπ/3)

Adamm: 3sinx=2cos²x 3sinx=2−2sin²x 2sin²x+3sinx−2=0 Δ=9+16=25

	−3±5
sinx=
	4

	1
sinx=−2 lub sinx=
	2

	1
sinx=		=sin(π/6)
	2

x=π/6+2kπ lub x=5π/6+2kπ

Adamm:

	1
sin2x≤
	2

(sinx−√2/2)(sinx+√2/2)≤0 −√2/2≤sinx≤√2/2 z rysunku wiemy że x∊(−π/4+2kπ;π/4+2kπ)∪(3π/4+2kπ; 5π/4+2kπ)

Adamm: tam powinny być przedziały domknięte

Adamm: (3π/4+2kπ; 5π/4+2kπ) i ten przedział jest źle, powinno być x∊<−π/4+2kπ;π/4+2kπ>∪<7π/4+2kπ; 9π/4+2kπ>

Adamm: czekaj, <−π/4+2kπ;π/4+2kπ>∪<7π/4+2kπ; 9π/4+2kπ> to są te same przedziały, przepraszam za zamiszanie, jednak powinno być x∊<−π/4+2kπ;π/4+2kπ>∪<3π/4+2kπ; 5π/4+2kπ>