Rozwiązywanie trójkątów prostokątnych Wujas: Jedna z przyprostokatnych trójkąta jest o 2 krótsza od przeciwprostokatnej. Środkowa poprowadzona do tej przyprostokatnej ma długość 2√6 Oblicz miary kątów ostrych tego trójkąta i długość jego pozostałych środkowych.

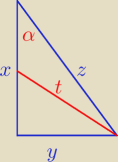
PW: Z twierdzenia Pitagorasa zastosowanego w dwóch widocznych trójkątach prostokątnych x² + y² = z²

	x
(		)2 + y2 = t2;
	2

Po odjęciu stronami dostajemy

	3
		x2 = z2 − t2.
	4

\Wiemy, że z = x+2 i t = 2√6, a więc

	3
		x2 = (x+2)2 − (2√6)2.
	4

Rozwiązaniem tego równania kwadratowego jest x = 8 (ale sprawdź rachunki!). Wynika stąd, że

	8		4
cosα =		=
	8+2		5

− jest to jednocześnie sinus drugiego z kątów ostrych. Znalezienie pozostałych środkowych nie powinno sprawić kłopotu − poprowadzona do boku y za pomocą twierdzenia Pitagorasa, a poprowadzona do przeciwprostokątnej − z twierdzenia kosinusów.

Eta: Jeżeli x=8 i z=10 to środkowa t ≠ 2√6

PW:

	4		2
Oczywiście pomyliłem się, powinno być x = 4, a więc cosα =		=
	4+2		3

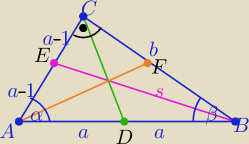
Eta: a>1 (a−1)²+b²=s² i [2(a−1)]²+b²=4a² a²−2a+b²−23=0 i b²−8a+4=0 ⇒ b²= 8a−4 to a²+6a−27=0 ⇒(a+9)(a−3)=0 ⇒ a=3 zatem : |AB|=6 , |AC|= 4 , |BC|= 2√5 środkowe: |CD|=a= 3 i |AF|= √4²+(√5)²= √21 sinα=cosβ=............⇒ α=.... β=....

PW: Mądre oznaczenia

PW: ... ale nie rozumiem dlaczego |CD| = a.

Eta: Żarty ?

PW: Nie, może mam zaćmienie. Napisz, niech się nie dręczę.

Jack: ja tez tego nie wiem

PW: O licho, promień okręgu opisanego!

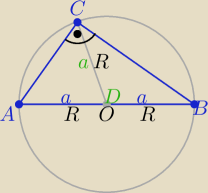
Eta: Rysunek dla właściciela postu ... gdyby zadał takie (banalne) pytanie dla PW

Jack: jaaa, faktycznie

PW: Nabieram coraz większego przekonania, że to Ty, Eta, wymyślasz te zadania.

Eta:

Eta: O co Ty PW mnie podejrzewasz? Leniwa ostatnio jestem bo mi korzonki dokuczają ( nie mylić z "korzonkiem"