Geometria analityczna Nowy: Odcinek o koncach c(4,2) d(2,−3) jest dłuższą podstawą trapezu. Krótsza podstawa AB jest dra razy krótsza od odcinka CD, a jej środkiem jest punkt S(2;2,5). Oblicz współrzędne pozostałych wierzchołków trapezu.

===: − długość odcinka |CD| − współczynnik kierunkowy prostej przechodzącej przez C i D − równanie prostej zawierającej dłuższą podstawę − współrzędne punktów A i B

nowy : mam długość odcinka CD, równanie prostej z dłuższą podstawą y=⁵₂x−8 ale co dalej ?

Tadeusz: Wykorzystaj info, że krótsza podstawa jest dwa razy krótsza od CD

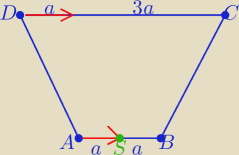
Eta: Proste rozwiązanie Za pomocą wektorów ( w zapisach pomijam "strzałki" dla łatwości →

	1
DC=[2,5] oraz z treści zadania : AS=		DC
	4

	1		5
to: AS=[2−xA, 2,5−yA] = [		,		]
	2		4

	1		5
⇒ 2−xA=		i 2,5−yA=		⇒ xA=..... i yA=....
	2		4

to x_B= 2x_S−x_A=..... i y_B= 2y_S−y_A =.....