dobry wieczor. prosze o pomoc w rozwiazaniu liczby zespolonej, zapisaniu w posta deluk: dobry wieczor. prosze o pomoc w rozwiazaniu liczby zespolonej, zapisaniu w postaci trygonometrycznej, obliczeniem jej modulu |z| i arg z

	−2+2i
z=(		)12
	1−√3i

PW: Wskazówka (−1 + i)² = (−1)² + 2•(−1)•i + i² = 1 − 2i − 1 = −2i, a więc obliczenie 12. potęgi licznika nie sprawia trudności. Pomyśl, czy mianownik też ma taką przyjemną właściwość.

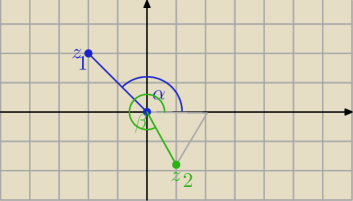
Mila: z₁=−2+2i |z₁|=√2²+2²=√8

	3π
α=		łatwo doczytac z ukł. wsp.
	4

	3π		3π
z1=2√2 *(cos		+i sin		}
	4		4

z₂=1−√3 |z₂|=√1+3=2 II sposób na wyznaczenie argumentu

	1		√3
cosβ=		i sinβ=−
	2		2

kąt IV ćwiartki

	π		5π
β=2π−		=
	3		3

	5π		5π
z2=2*(cos		+i sin		)
	3		3

	z1
(		)12=
	z2

	√8		3π   3π   (cos +i sin )12   4   4
=(		)12*		=
	2		5π   5π   (cos +i sin )12   3   3

	86		3π   3π   (cos12* +i sin12* )   4   4
=		*		=
	212		5π   5π   (cos12* +i sin12* )   3   3

	218		(cos9π+i sin9π)
=		*		=
	212		(cos20π+i sin20π

=2⁶*(cos(−11π+i sin (−11π)= =2⁶*(cos(−11π+12π)+i sin(−11π+12π) =2⁶*(cosπ+i sin π) Postać wykładnicza z=2⁶*eⁱπ=64e^iπ

PW: Dla pokazania, że można "algebraicznie" dokończmy pomysł z 21:46. Licznik jest równy 2¹²(−2i)⁶ = − 2¹⁸. Jak łatwo zauważyć (1 − √3i)³= 1 − 3√3i + 3(√3i)² − (√3i)³ = 1 − 3√3i − 9 + 3√3i = − 8, wobec tego mianownik jest równy (− 8)⁴ = 2¹². Badana liczba jest więc ilorazem

	− 218
		= − 26 = − 64.
	212

Jej moduł jest równy |−64| = 64, argument oczywiście jest równy π, postać trygonometryczna 64(cosπ + i sinπ), postać wykładnicza 64e^iπ. Warto liczby −1+i oraz 1−√3i zapamiętać jako łatwe do potęgowania metodą algebraiczną.