Optymalizacja, dziedzina funkcji, WSiP nielubiewymyslacnikow: Zadanie optymalizacyjne! Dane są dwie funkcje f(x)= |x−1|−2 i g(x)= 2mx , razem tworzą trójkąt w układzie współrzędnych. W rozwiązaniu zadania (w zbiorze) jest napisane: "Łatwo zauważyć, że wykresy funkcji mają dwa punkty wspólne gdy m ∊ (− ¹₂, ¹₂) jeżeli m∊R\(−¹₂, ¹₂) to funkcja f(x) i g(x) mają jeden punkt wspólny, nie tworzą więc obszaru wspólnego". Czy ktoś mógłby wytłumaczyć skąd wzięło się założenie m∊(− ¹₂, ¹₂) ?

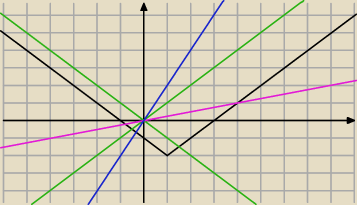
Jerzy: Czarna y = Ix − 1I − 2 Zielone: y = x i y = −x ( m = −1,2 lub m = 1/2) Jeśli m ∊ (−1/2;1/2) , to prosta g (różowa ) , leży pomiedzy zielonymi prostymi tak,że tnie f w dwóch punktach Jeśli m jest poza przedziałem , to prosta ( niebieska ) tnie f tylko w jednym punkcie