Zadanie
Input:
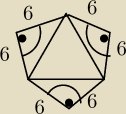
Rysunek obok przedstawia siatkę bryły:
a) Korzystając z wymiarów podanych na rysunku oblicz jej pole powierzchni całkowitej
b) Oblicz cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy
27 paź 14:22
Jerzy:
I gdzie masz problem ?
27 paź 14:57
piotr1973: P= 3*6*6/2+(62+62)√3/4
cos = (√62+62/6)/(6√2/2) = 1/3
27 paź 15:30
Input:
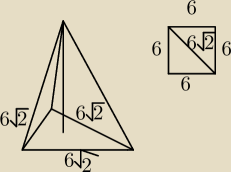
| | a2√3 | |
Ja obliczyłem to że tak że pole podstawy to trojkat rownoboczny wiec pole |
| wiec |
| | 4 | |
| (6 √2)2√3 | | 72 √3 | |
| = |
| = 18 √3 |
| 4 | | 4 | |
z pitagorasa trojkat rownoramienny na pol
6
2 = (3
√2)
2 + h
2
36 = 18 + h
2
h
2 = 18
h =
√18
| | 1 | |
a pozostale to rownoramienne: 3 * |
| *6*√18 = √18 + 18 √3 |
| | 2 | |
Nie wiem dlaczego to jest źle...
27 paź 16:18
Input: Co robie źle
27 paź 16:18
Input: Czy pole podstawy mam chociaż dobrze?
27 paź 21:29
5-latek: Dodaj jeszcze pole podstawy
27 paź 21:32
Input: 18√3 + 9√18 /*√3
54 + 9√54 = 63√54
...
Dobrze?
27 paź 21:43
27 paź 21:51
Input:
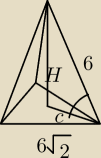
A teraz jak z tym cosinusem?
| | 2 | | 2 | |
Bo zauważyłem że c bedzie wynosic 6 √2 * |
| bo to |
| wysokości trójkąta |
| | 3 | | 3 | |
równobocznego.
No i wychodzi 4
√2.
I teraz cos:
I chyba coś jest źle bo wynik inny niż dał
piotr1973
29 paź 11:18
Adamm: 6√2 to bok, nie wysokość
29 paź 11:32
Input: A no tak wybacz.
h =
√18 czyli 3
√2
29 paź 11:39
Input: Czy to jest dobry wynik dla cosinusa?
29 paź 11:39
Adamm: nie myl wysokości boku z wysokością podstawy
29 paź 11:44
Adamm: raczej wysokości ściany bocznej zamiast ściany boku
29 paź 11:46
Input: Ale to jest wysokość trójkąta równobocznego czyli podstawy, a nie ściana boczna.
Bo krawędź ściany mam = 6. Czyli to c na moim rysunku chyba tylko sie da z 2/3 wysokości

29 paź 11:52
Jerzy:
| | √2 | |
Masz dobrze .. .cosα = |
| |
| | 3 | |
29 paź 11:56
Adamm: patrz na swój post 16:18, policzyłeś tam wysokość ściany bocznej, a nie podstawy
29 paź 11:58
Adamm: | | 6√2*√3 | |
wysokość podstawy to h= |
| =3√6 |
| | 2 | |
29 paź 12:04
Input: Adamm, masz rację − dzięki

29 paź 12:26
 Rysunek obok przedstawia siatkę bryły:
a) Korzystając z wymiarów podanych na rysunku oblicz jej pole powierzchni całkowitej
b) Oblicz cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy
Rysunek obok przedstawia siatkę bryły:
a) Korzystając z wymiarów podanych na rysunku oblicz jej pole powierzchni całkowitej
b) Oblicz cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy
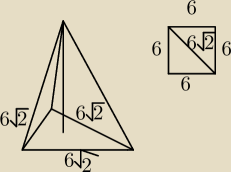
 A teraz jak z tym cosinusem?
A teraz jak z tym cosinusem?


