Zadanie dziwna odpowiedź Input: Krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długość 3cm, a ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 60^o. Oblicz objętość ostrosłupa...

	3 √3
Robie wszystko fajnie, wychodzi trójkąt o kątach 30,60,90 więc wysokość będzie		a,
	2

	9 √3		27 √3
pole podstawy to 6 *		czyli		.
	4		2

	1		27 √3		3 √3		81
A więc Pole całkowite to		*		*		i wychodzi		no bo
	3		2		2		4

pierwiastkek razy pierwiastek daje w tym przypadku 3.

	81 √3
Dlaczego zatem w odpowiedzi jest: Pc =
	4

piotr1973: Pole podstawy

	32√3
Pp = 6*
	4

	3√3
h=		* tg(60o) = 9/2
	2

	1		32√3		9
V=		6*		*
	3		4		2

Input: Dzięki Piotr. Powiesz mi jeszcze dlaczego wysokość mnożymy przez wynik z tg60 czyli pierwiastek z 3 bo jest to dla mnie tajemnica...

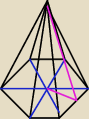piotr1973: kąt, którym jest mowa w treści zadania jest równy kątowi między wysokością trójkąta ściany bocznej i wysokością trójkąta równobocznego powstałego po podzieleniu ośmiokąta foremnego podstawy (różowy kąt)