Stereometria Sasasa: W ostrosłupie prawidłowym czworokątnym wysokość i krawędź boczna ostrosłupa tworzy trójkąt równoboczny o polu równym 8². Oblicz objętość tego ostrosłupa. Takie coś jest wgl możliwe?

Sasasa: 8√2*

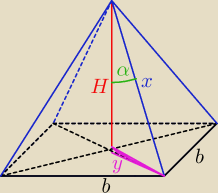
Jack: Skoro to ostroslup prawidlowy czworokatny to w podstawie jest kwadrat,

	b√2
nazwijmy jego bok "b", wtedy y =
	2

Skoro wysokosci krawedz boczna tworza trojkat rownoboczny, to H = x = y

	b√2
ale wiemy, ze y =		zatem
	2

	b√2
H = x =
	2

	a2√3
Wzor na pole trojkata rownobocznego =
	4

w naszym przypadku :

	b√2   ( )2√3   2		b2   √3 2		b2√3
P =		=		=
	4		4		8

wiemy, ze to pole wynosi 8√2 zatem

b2√3
	= 8√2
8

b²√3 = 64√2

	64√2		64√6
b2 =		=
	√3		3

	64√6		√6		√√6		√√18
b = √		= √64 * √		= 8*		= 8*		=
	3		3		√3		3

	8
=		√3√2
	3

	1
Objetosc ostroslupa to V =		* Pp * H
	3

	1		b√2		b3√2
zatem V =		* b2 *		=
	3		2		6

V = ... bardzo dziwne liczby wyszly...

Eta: ? Popraw treść zadania