m Arcani: Dany jest wierzchołek kwadratu A(1,−3) i jedna z jego przekątnych k: 2x−y=0. Wyznaczyć równania boków kwadratu

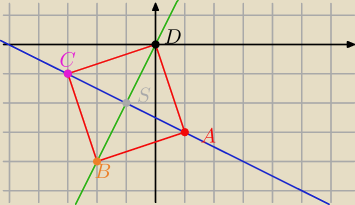
Jack: prosta k : y = 2x jest przekatna kwadratu, zatem prosta prostopadla do niej utworzy druga przekatna, jezeli bedzie przechodzic przez punkt A. zatem rownanie prostej prostopadlej do k, nazwijmy ja l

	1
prosta l : y = −		x + b
	2

podstawiajac punkt A

	1
−3 = −		* 1 + b /*2
	2

	5
−6 = − 1 + 2b −−−−> b = −
	2

	1		5
l : y = −		x −
	2		2

Proste k i l przecinaja sie w punkcie :

	1		5
−		x −		= 2x / *2
	2		2

−x − 5 = 4x −−−−> x = −1 y = −3 nazwijmy go S, zatem S(−1,−2) Dalej pomysl

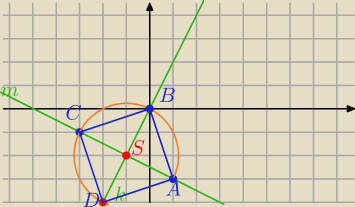Mila: A(1,−3) k: y=2x Przekątne w kwadracie są prostopadłe, równe i dzielą się na połowy. m⊥k i A∊m

	1
y=−		x+b
	2

	1		5
−3=−		*1+b, b=−
	2		2

	1		5
m: y=−		x−
	2		2

S− punkt przecięcia przekątnych

	1		5
−		x−		=2x
	2		2

x=−1 i y=−2 S=(−1,−2) − środek przekątnej C=(a,b)

	a+1		b−3
−1=		−2=		⇔a=−3 i b=−1
	2		2

C=(−3,−1) R=|SA|=√2²+1²=√5 (x+1)²+(y+2)²=5 y=2x rozwiązując układ otrzymamy wsp . B i D x=0 i y=0⇒B=(0,0) x=−2 i y=−4⇔D=(−2,−4) Pisz równania: