Liczby zespolone - graficzna interpretacja Gravity: 2|z+1|<|z²−z−2|≤3|z−2| Rozwiązałem to ale nie jestem pewien czy dobrze. Ogólnie to liczyłem osobno lewą i prawą stronę Odpowiednio dzieląc przez |z+1| i |z−2| i żeby nie dzielić przez 0 to z lewej strony wyrzuciłem z=−1 a z prawej z=2. Tak się to powinno zrobić?

Gravity: Ktoś, coś?

Janek191: z = x + y i z + 1 = x + 1 + y i z − 2 = x − 2 + y i Oblicz moduły i działaj

Mila: z²−z−2=0 Δ=9

	1−3		1+3
z1=		lub z2=
	2		2

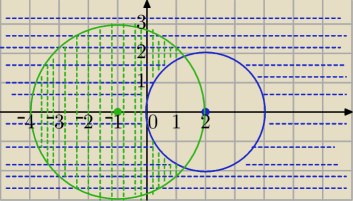
z₁=−1 lub z₂=2 2|z+1|≤|z²−z−2|≤3|z−2|⇔ 2*|z+1|≤|z+1|*|z−2| i |z+1|*|z−2|≤3|z−2|⇔ 2*|z+1|−|z+1|*|z−2|≤0 i |z+1|*|z−2|−3|z−2|≤0⇔ |z+1|*(2−|z−2|)≤0 i |z−2|*(|z+1|−3)≤0 wiadomo, że |z+1|≥0 i |z−2|≥0 ⇒(2−|z−2|)≤0 i (|z+1|−3)≤0⇔ |z−2|≥2 i |z+1|≤3 lub rozwiązujesz układ nierówności 2√(x+1)²+y²≤√(x+1)²+y²*√(x−2)²+y²≤3*√(x−2)²+y²