Rachunek różniczkowy Donna: W półkole o promieniu 2 wpisano trójkąty równoramienne, których wierzchołek leży w środku koła. Pole największego z wpisanych trójkątów wynosi:

	√3
A. 1 B. √2 C.		D. 2
	2

Wywnioskowałam, że trójkąty będą miały ramiona równe 2, ale to wszystko... Pomoże ktoś?

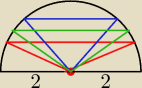Jack: Rozpatrujemy trojkaty zbudowe w ten sposob (patrz rysunek) kazdy jest rownoramienny o ramionach dlugosci 2. wykorzystajmy wzor na pole :

	1
P =		a*b*sin α , gdzie a,b to boki trojkata, a α to kat miedzy tymi bokami
	2

u nas a = b = 2

	1
zatem P =		* 2 * 2 * sin α = 2 sin α
	2

Naszym zadaniem jest znalezc najwieksza wartosc kata α. zatem pochodna Oczywiscie rozpatrujemy kat α ∊ (0;180) P (α) = 2sinα P ' (α) = 2cosα 2 cos α = 0 cos α = 0 α = 90^o i tu osiagamy ekstremum zatem P_max = 2 sin 90 = 2 * 1 = 2 (mam nadzieje ze nic nie pominalem)

Donna: Dziękuję bardzo!