Zadanie optymalizacyjne Whale: Na hiperboli o równaniu y=4/x (gdzie x nie może się równać 0) obrano dwa punkty A(1,4), B(2,2). Znajdź punkt C o ujenych współrzędnych należący do tej hiperboli, aby pole trójkąta było jak najmniejsze. Jakaś podpowiedź?

Janek191:

	4
C = ( x, y) = ( x,		)
	x

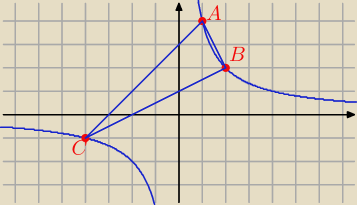
A = (1, 4) B = ( 2, 2) →

	4
CA = [ 1 − x, 4 −		]
	x

→

	4
CB = [ 2 − x, 2 −		]
	x

Pole Δ ABC → →

	4		4
P = 0, 5 I det ( CA , CB ) I = 0, 5* I ( 1 − x)*( 2 −		) − (2 − x)*( 4 −		) I =
	x		x