parametr m Jaehyo:

	1−x2
dane jest równanie z niewiadomą x:		=m+3 , m należy do l. rzeczywistych. i muszę
	|x+1|

wyznaczyć liczbę rozwiązań w zależności od parametru m. I zrobiłem tak że: jeśli x>−1 to m<5 jeśli x<−1 to wyszło że m<1 i teraz w odp. powinno być że jeśli m<1 to równanie ma 2 r. m∊<1;5) to równanie ma 1 r. m≥5 równanie ma 0 r. i nie mam pojęcia skąd się bierze odp. i proszę pomoc w wytłumaczeniu

5-latek:

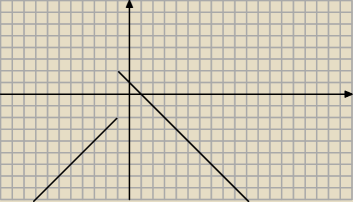
	1−x2
Taki wyszedl w tym edytorze wykres funkcji f(x)=
	|x+1|

Teraz tnij go prosta y=m+3

5-latek: Musisz zaznaczyc ze dla x≠−1

Jaehyo: o boże, dobra, ogarnąłem, dzięki xd

Mila:

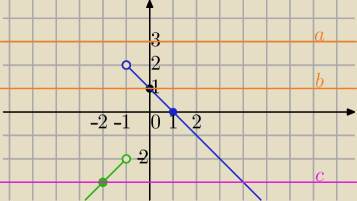
	(1−x)*(1+x)
f(x)=		i x≠−1
	|x+1|

1) |x+1|=x+1 dla x>−1 wtedy:

	(1−x)*(1+x)
f(x)=		⇔ f(x)=1−x
	x+1

|x+1|=−x−1 dla x<−1 wtedy

	(1−x)*(1+x)
f(x)=		⇔f(x)=x−1
	−(x+1)

f(x)=m+3 a) m+3≥2 ⇔m≥−1 − brak rozwiązań (przykład na wykresie) b) −2≤m+3<2 /−3 ⇔ −5≤m<−1 jedno rozwiązanie c) m+3<−2 ⇔m<−5 dwa rozwiązania Odpowiedź taka jak w książce jest dla równania f(x)=m−3