Zadanie z ciągów Jacek: Dany jest ciąg o wzorze ogólnym an=n³+40n²−25n. Dla jakich n jest spełniony warunek an>1000?

Adamm: a_n>1000 n³+40n²−25n−1000>0 (n−5)(n+5)(n+40)>0 dla n>5 mamy rozwiązanie

Mila: n³+40n²−25n>1000⇔ n∊N₊ n³+40n²−25n−1000>0 w(5)=125+40*25−25*5−1000=0 schemat Hornera 1 40 −25 −1000 n=5 1 45 200 0 n³+40n²−25n−1000=(n−5)*(n²+45n+200) Δ=2025−800=1225

	−45−35		80		−45+35
n=		=−		=−40 lub n=		=−5
	2		2		2

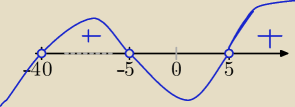
n³+40n²−25n−1000=(n−5)*(n+5)*(n+40) (n−5)*(n+5)*(n+40)>0 i n∊N₊⇔ n>5