Funkcje Donna: Jest funkcja dana wzorem f(x) = √ x² −6x+9 + √x² . Rozwiąż f(x)≥6 i zapisz zbiór jej rozwiązań z użyciem wartości bezwzględnej. Zrobiłam tyle: zał.: (x−3)² ≥ 0 i x² ≥ 0 Df= x∊<0;∞) I. x∊<0;3) −x+3+x≥6 3≥6 sprzeczność II. x∊<3;∞) x−3+x≥6 2x≥9//2

	9
x≥
	2

	9
x∊<		;∞)
	2

Teraz mam problem, bo nie wiem jak mam to zapisać za pomocą wartości bezwzględnej. Pomoże ktoś?

Adamm: dziedzina jest źle

Omikron: Zła dziedzina. Kwadrat dowolnej liczby rzeczywistej jest nieujemny. Czarnego Jerzego ignoruj, to troll.

Ajtek: Coś mi się nie podoba dziedzina.

Adamm: |x−3|+|x|≥6 rozwiąż, dziedzina rzeczywiste

Omikron: Kiedy wyniesiesz się raz na zawsze z tego forum

Tadeusz: jeśli znasz wzory skróconego mnożenia to dziedzina jest oczywista f(x)=√(x−3)²+√x² f(x)=|x−3|+|x| itd

Donna: Okay. Zmieniłam dziedzinę na całe R. I wychodzą mi takie rozwiązania:

	3
1. x∊(−∞; −		>
	2

	9
2. x∊<		;∞)
	2

Czy teraz będzie dobrze?

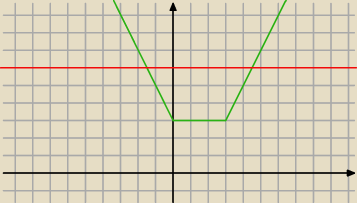
Tadeusz: ok